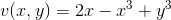All Complex Analysis Resources
Example Questions
Example Question #1 : Analytic And Harmonic Functions
Find a Harmonic Conjugate 
Possible Answers:
Correct answer:
Explanation:


where 
Example Question #2 : Analytic And Harmonic Functions
Given 

Possible Answers:
Nowhere
The Entire Complex Plane
Correct answer:
Nowhere
Explanation:
Rewriting 
So this implies that
where
Therefore, checking the Cauchy-Riemann Equations, we have that
So the Cauchy-Riemann equations are never satisfied on the entire complex plane, so 
Kevin
Certified Tutor
Certified Tutor
Southeast Missouri State University, Bachelors, Pure and Applied Mathematics. Southeast Missouri State University, Masters, M...
Melanie
Certified Tutor
Certified Tutor
Armstrong State College, Bachelor of Education, Early Childhood Education. Lesley University, Masters in Education, Science T...
All Complex Analysis Resources
Popular Subjects
French Tutors in Washington DC, GMAT Tutors in Dallas Fort Worth, Physics Tutors in Philadelphia, SAT Tutors in Houston, Statistics Tutors in Boston, GMAT Tutors in Denver, SSAT Tutors in Atlanta, French Tutors in New York City, ACT Tutors in Washington DC, MCAT Tutors in Philadelphia
Popular Courses & Classes
ACT Courses & Classes in Houston, MCAT Courses & Classes in Los Angeles, GMAT Courses & Classes in San Diego, SSAT Courses & Classes in Boston, ACT Courses & Classes in Miami, Spanish Courses & Classes in Phoenix, SSAT Courses & Classes in Houston, ACT Courses & Classes in Washington DC, GMAT Courses & Classes in Houston, LSAT Courses & Classes in New York City
Popular Test Prep
ACT Test Prep in Houston, SSAT Test Prep in San Francisco-Bay Area, SAT Test Prep in Seattle, ACT Test Prep in Miami, SAT Test Prep in Phoenix, LSAT Test Prep in Phoenix, ISEE Test Prep in Washington DC, SSAT Test Prep in Seattle, SSAT Test Prep in San Diego, GMAT Test Prep in San Diego