All Common Core: High School - Statistics and Probability Resources
Example Questions
Example Question #9 : Interpret Difference In Shape Of Data Distribution: Ccss.Math.Content.Hss Id.A.3
Two students have taken ten math tests in the first quarter of the school year. Joe received the following scores on these ten tests:
Melissa obtained the following ten scores:
Predict which student will get the higher score on the next test.
Cannot be determined
Melissa
Joe
Both students will get the same score
Melissa
In order to solve this problem, we need to make an inference. An inference is made using observations in prior knowledge. If we have multiple observations, then we can make better inferences. Let's develop our inference using the information provided for Joe and Melissa.
Joe obtained the following scores:
Let's tabulate this data into a histogram.

Let's find the mean of this data series. The mean is the arithmetic average of the data set. The mean is found by adding up the values and dividing the total by the number of values in the series.
Now, let's calculate the standard deviation of the data series. The standard deviation for an entire population is found using the following formula:
First, we need to calculate how much each value deviates from the mean. We will do this by subtracting the mean from each value and squaring the difference.
Second, we will find the variance by adding up this values and dividing by the number of values in the series.
Last, the standard deviation equals the square root of the variance.
Now, we need to focus on Melissa's scores:
Let's tabulate this data into a histogram.

Let's find the mean of this data series. The mean is the arithmetic average of the data set. The mean is found by adding up the values and dividing the total by the number of values in the series.
Now, let's calculate the standard deviation of the data series. The standard deviation for an entire population is found using the following formula:
First, we need to calculate how much each value deviates from the mean. We will do this by subtracting the mean from each value and squaring the difference.
Second, we will find the variance by adding up this values and dividing by the number of values in the series.
Last, the standard deviation equals the square root of the variance.

Now, let's review our data and calculations.
Given the information, we can see that Melissa's scores have a higher mean value and a smaller standard deviation for the set of values. This means that her scores are—on average—higher than Joe's and they vary less; therefore, we can predict that she will score higher on the test. Some may argue that Joe will score higher because of his one very high grade. It is true that he has the highest single grade between the two students; however, this is an outlier in the data. His lower mean score and higher tendency to vary between tests indicates that he will most likely not score higher than Melissa.
Example Question #41 : Interpreting Categorical & Quantitative Data
Two students have taken ten math tests in the first quarter of the school year. Joe received the following scores on these ten tests:
Melissa obtained the following ten scores:
Predict which student will get the higher score on the next test.
Cannot be determined
Joe
Both students will get the same score
Melissa
Melissa
In order to solve this problem, we need to make an inference. An inference is made using observations in prior knowledge. If we have multiple observations, then we can make better inferences. Let's develop our inference using the information provided for Joe and Melissa.
Joe obtained the following scores:
Let's tabulate this data into a histogram.

Let's find the mean of this data series. The mean is the arithmetic average of the data set. The mean is found by adding up the values and dividing the total by the number of values in the series.
Now, let's calculate the standard deviation of the data series. The standard deviation for an entire population is found using the following formula:
First, we need to calculate how much each value deviates from the mean. We will do this by subtracting the mean from each value and squaring the difference.
Second, we will find the variance by adding up this values and dividing by the number of values in the series.
Last, the standard deviation equals the square root of the variance.
Now, we need to focus on Melissa's scores:
Let's tabulate this data into a histogram.

Let's find the mean of this data series. The mean is the arithmetic average of the data set. The mean is found by adding up the values and dividing the total by the number of values in the series.
Now, let's calculate the standard deviation of the data series. The standard deviation for an entire population is found using the following formula:
First, we need to calculate how much each value deviates from the mean. We will do this by subtracting the mean from each value and squaring the difference.
Second, we will find the variance by adding up this values and dividing by the number of values in the series.
Last, the standard deviation equals the square root of the variance.

Now, let's review our data and calculations.
Given the information, we can see that Melissa's scores have a higher mean value and a smaller standard deviation for the set of values. This means that her scores are—on average—higher than Joe's and they vary less; therefore, we can predict that she will score higher on the test. Some may argue that Joe will score higher because of his one very high grade. It is true that he has the highest single grade between the two students; however, this is an outlier in the data. His lower mean score and higher tendency to vary between tests indicates that he will most likely not score higher than Melissa.
Example Question #42 : Interpreting Categorical & Quantitative Data
Two students have taken ten math tests in the first quarter of the school year. Joe received the following scores on these ten tests:
Melissa obtained the following ten scores:
Predict which student will get the higher score on the next test.
Cannot be determined
Both students will get the same score
Joe
Melissa
Melissa
In order to solve this problem, we need to make an inference. An inference is made using observations in prior knowledge. If we have multiple observations, then we can make better inferences. Let's develop our inference using the information provided for Joe and Melissa.
Joe obtained the following scores:
Let's tabulate this data into a histogram.

Let's find the mean of this data series. The mean is the arithmetic average of the data set. The mean is found by adding up the values and dividing the total by the number of values in the series.
Now, let's calculate the standard deviation of the data series. The standard deviation for an entire population is found using the following formula:
First, we need to calculate how much each value deviates from the mean. We will do this by subtracting the mean from each value and squaring the difference.
Second, we will find the variance by adding up this values and dividing by the number of values in the series.
Last, the standard deviation equals the square root of the variance.
Now, we need to focus on Melissa's scores:
Let's tabulate this data into a histogram.

Let's find the mean of this data series. The mean is the arithmetic average of the data set. The mean is found by adding up the values and dividing the total by the number of values in the series.
Now, let's calculate the standard deviation of the data series. The standard deviation for an entire population is found using the following formula:
First, we need to calculate how much each value deviates from the mean. We will do this by subtracting the mean from each value and squaring the difference.
Second, we will find the variance by adding up this values and dividing by the number of values in the series.
Last, the standard deviation equals the square root of the variance.
Now, let's review our data and calculations.
Given the information, we can see that Melissa's scores have a higher mean value and a smaller standard deviation for the set of values. This means that her scores are—on average—higher than Joe's and they vary less; therefore, we can predict that she will score higher on the test. Some may argue that Joe will score higher because of his one very high grade. It is true that he has the highest single grade between the two students; however, this is an outlier in the data. His lower mean score and higher tendency to vary between tests indicates that he will most likely not score higher than Melissa.
Example Question #43 : Interpreting Categorical & Quantitative Data
Two students have taken ten math tests in the first quarter of the school year. Joe received the following scores on these ten tests:
Melissa obtained the following ten scores:
Predict which student will get the higher score on the next test.
Cannot be determined
Joe
Both students will get the same score
Melissa
Joe
In order to solve this problem, we need to make an inference. An inference is made using observations in prior knowledge. If we have multiple observations, then we can make better inferences. Let's develop our inference using the information provided for Joe and Melissa.
Joe obtained the following scores:
Let's tabulate this data into a histogram.

Let's find the mean of this data series. The mean is the arithmetic average of the data set. The mean is found by adding up the values and dividing the total by the number of values in the series.
Now, let's calculate the standard deviation of the data series. The standard deviation for an entire population is found using the following formula:
First, we need to calculate how much each value deviates from the mean. We will do this by subtracting the mean from each value and squaring the difference.
Second, we will find the variance by adding up this values and dividing by the number of values in the series.
Last, the standard deviation equals the square root of the variance.
Now, we need to focus on Melissa's scores:
Let's tabulate this data into a histogram.

Let's find the mean of this data series. The mean is the arithmetic average of the data set. The mean is found by adding up the values and dividing the total by the number of values in the series.
Now, let's calculate the standard deviation of the data series. The standard deviation for an entire population is found using the following formula:
First, we need to calculate how much each value deviates from the mean. We will do this by subtracting the mean from each value and squaring the difference.
Second, we will find the variance by adding up this values and dividing by the number of values in the series.
Last, the standard deviation equals the square root of the variance.
Now, let's review our data and calculations.
Given the information, we can see that Joe's scores have a higher mean value and a smaller standard deviation for the set of values. This means that his scores are—on average—higher than Melissa's and they vary less; therefore, we can predict that he will score higher on the test. Some may argue that Melissa will score higher because of his one very high grade. It is true that she has the highest single grade between the two students; however, this is an outlier in the data. Her lower mean score and higher tendency to vary between tests indicates that she will most likely not score higher than Joe.
Example Question #44 : Interpreting Categorical & Quantitative Data
Two students have taken ten math tests in the first quarter of the school year. Joe received the following scores on these ten tests:
Melissa obtained the following ten scores:
Predict which student will get the higher score on the next test.
Cannot be determined
Joe
Melissa
Both students will get the same score
Melissa
In order to solve this problem, we need to make an inference. An inference is made using observations in prior knowledge. If we have multiple observations, then we can make better inferences. Let's develop our inference using the information provided for Joe and Melissa.
Joe obtained the following scores:
Let's tabulate this data into a histogram.

Let's find the mean of this data series. The mean is the arithmetic average of the data set. The mean is found by adding up the values and dividing the total by the number of values in the series.
Now, let's calculate the standard deviation of the data series. The standard deviation for an entire population is found using the following formula:
First, we need to calculate how much each value deviates from the mean. We will do this by subtracting the mean from each value and squaring the difference.
Second, we will find the variance by adding up this values and dividing by the number of values in the series.
Last, the standard deviation equals the square root of the variance.
Now, we need to focus on Melissa's scores:
Let's tabulate this data into a histogram.

Let's find the mean of this data series. The mean is the arithmetic average of the data set. The mean is found by adding up the values and dividing the total by the number of values in the series.
Now, let's calculate the standard deviation of the data series. The standard deviation for an entire population is found using the following formula:
First, we need to calculate how much each value deviates from the mean. We will do this by subtracting the mean from each value and squaring the difference.
Second, we will find the variance by adding up this values and dividing by the number of values in the series.
Last, the standard deviation equals the square root of the variance.
Now, let's review our data and calculations.
Given the information, we can see that Melissa's scores have a higher mean value and a smaller standard deviation for the set of values. This means that her scores are—on average—higher than Joe's and they vary less; therefore, we can predict that she will score higher on the test. Some may argue that Joe will score higher because of his one very high grade. It is true that he has the highest single grade between the two students; however, this is an outlier in the data. His lower mean score and higher tendency to vary between tests indicates that he will most likely not score higher than Melissa.
Example Question #45 : Interpreting Categorical & Quantitative Data
Two students have taken ten math tests in the first quarter of the school year. Joe received the following scores on these ten tests:
Melissa obtained the following ten scores:
Predict which student will get the higher score on the next test.
Melissa
Joe
Cannot be determined
Both students will get the same score
Joe
In order to solve this problem, we need to make an inference. An inference is made using observations in prior knowledge. If we have multiple observations, then we can make better inferences. Let's develop our inference using the information provided for Joe and Melissa.
Joe obtained the following scores:
Let's tabulate this data into a histogram.

Let's find the mean of this data series. The mean is the arithmetic average of the data set. The mean is found by adding up the values and dividing the total by the number of values in the series.
Now, let's calculate the standard deviation of the data series. The standard deviation for an entire population is found using the following formula:
First, we need to calculate how much each value deviates from the mean. We will do this by subtracting the mean from each value and squaring the difference.
Second, we will find the variance by adding up this values and dividing by the number of values in the series.
Last, the standard deviation equals the square root of the variance.
Now, we need to focus on Melissa's scores:
Let's tabulate this data into a histogram.

Let's find the mean of this data series. The mean is the arithmetic average of the data set. The mean is found by adding up the values and dividing the total by the number of values in the series.
Now, let's calculate the standard deviation of the data series. The standard deviation for an entire population is found using the following formula:
First, we need to calculate how much each value deviates from the mean. We will do this by subtracting the mean from each value and squaring the difference.
Second, we will find the variance by adding up this values and dividing by the number of values in the series.
Last, the standard deviation equals the square root of the variance.

Now, let's review our data and calculations.
Given the information, we can see that Joe's scores have a higher mean value and a smaller standard deviation for the set of values. This means that his scores are—on average—higher than Melissa's and they vary less; therefore, we can predict that he will score higher on the test. Some may argue that Melissa will score higher because of his one very high grade. It is true that she has the highest single grade between the two students; however, this is an outlier in the data. Her lower mean score and higher tendency to vary between tests indicates that she will most likely not score higher than Joe.
Example Question #41 : Interpreting Categorical & Quantitative Data
Suppose that the population of a certain city is normally distributed with a mean of 10 million people and a standard deviation of 4 million people. What is the probability that the current population is between 8 million and 12 million people?
75%
34.13%
50%
68.26%
23.47%
68.26%
Example Question #2 : Fitting Data Sets To Normal Distribution And Estimating Area Under The Curve: Ccss.Math.Content.Hss Id.A.4
A social scientist performs an experiment testing the frequency and correlation of several demographics. She plots a histogram measuring income versus education level. She produces the following model:

Which of the following choices best describes this model?
Normal distribution
Negative/left skewed distribution
None of these
None of these
In order to solve this problem let's review the following distributions: normal, positive/right skewed, negative/left skewed, bimodal, and uniform.
Normal Distribution:

A normal distribution is also known as a bell curve. Data that form a bell curve have three primary characteristics: the data is single peaked meaning that it has a single mode, it is symmetrical, and contains no outliers.
Positive/Right Skewed Distribution
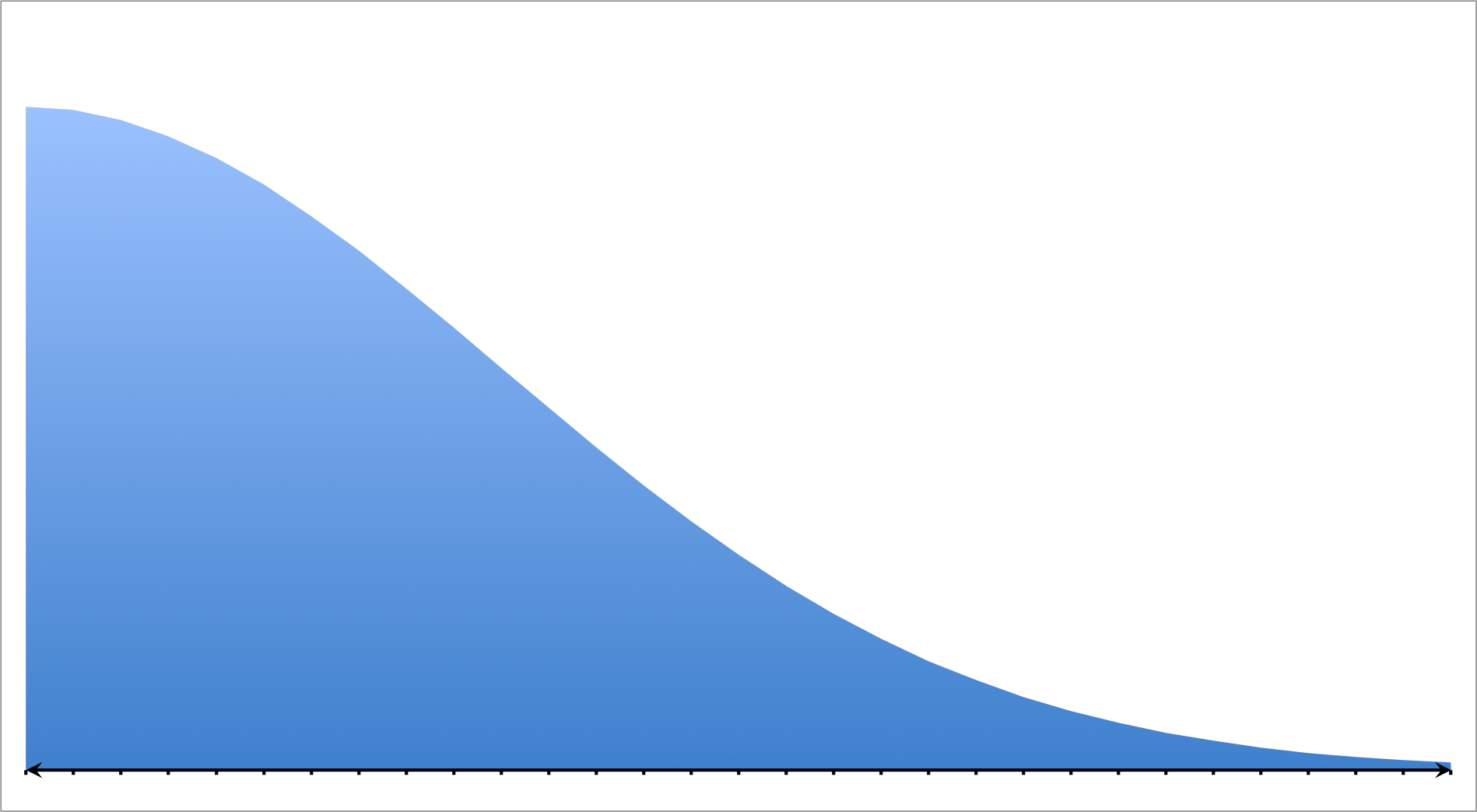
A positive or right skewed distribution has a longer tail on the right side due to outliers while the majority of the points are concentrated on the left side of the graph. In other words, the set favors probabilities on the left of the model.
Negative/Left Skewed Distribution

A negative or left skewed distribution has a longer tail on the left side due to outliers while the majority of the points are concentrated on the right side of the graph. In other words, the set favors probabilities on the right of the model.
Bimodal Distribution

In a bimodal distribution, there are two peaks due to several modes in the data set. These multiple central tendencies are the result of two or more favorable probabilities in the set.
Uniform Distribution

In a uniform distribution the data points form a a rectangle. These models are formed when data points possess a constant probability.
The model in the question does not match any of these; therefore, the correct answer is "none of these."
Example Question #41 : High School: Statistics & Probability
A student scores a 

Using this information, determine whether or not the student scored well on the SAT.
The student's score was average: similar to the mean.
The student scored poorly: below a single standard deviation of the mean.
The student scored well: above a single standard deviation of the mean.
The student scored very well: above two standard deviations of the mean.
The student scored very poorly: below two standard deviations of the mean.
The student scored very well: above two standard deviations of the mean.
In order to solve this problem, let's consider probabilities and the normal—bell curve—distribution. Given that all events are equally likely, probability is calculated using the following formula:
When probabilities of a given population are calculated for particular events, they can be graphed in a frequency chart or histogram. If they form a standard distribution, then the graph will form to the following shape:

This shape is known as a bell curve. In this curve, the mean is known as the arithmetic average and is represented as the peak. The mean alters the position of the graph. If the mean increases or decreases, then the graph shifts to the right or to the left respectively. The mean is denoted as follows:
On the other hand, the standard deviation is a calculation that indicates the average amount that each value deviates from the mean. When the standard deviation is changed then the shape of the graph is altered. When the standard deviation is decreased, the graph is taller and thinner. Likewise, when the standard deviation is increased, the graph becomes shorter and wider. It is important to note that 99.7 percent of all the values in a normal population exist between three standard deviations above and below the mean. It is denoted using the following annotation:
Now that we have discussed the components of the bell curve, let's consider the scenario presented in the question.
We know that the distribution of test scores follows a normal curve. We also know the following values:
We should first plot the data on a graph that follows the shape of a bell shaped curve with three standard deviations.
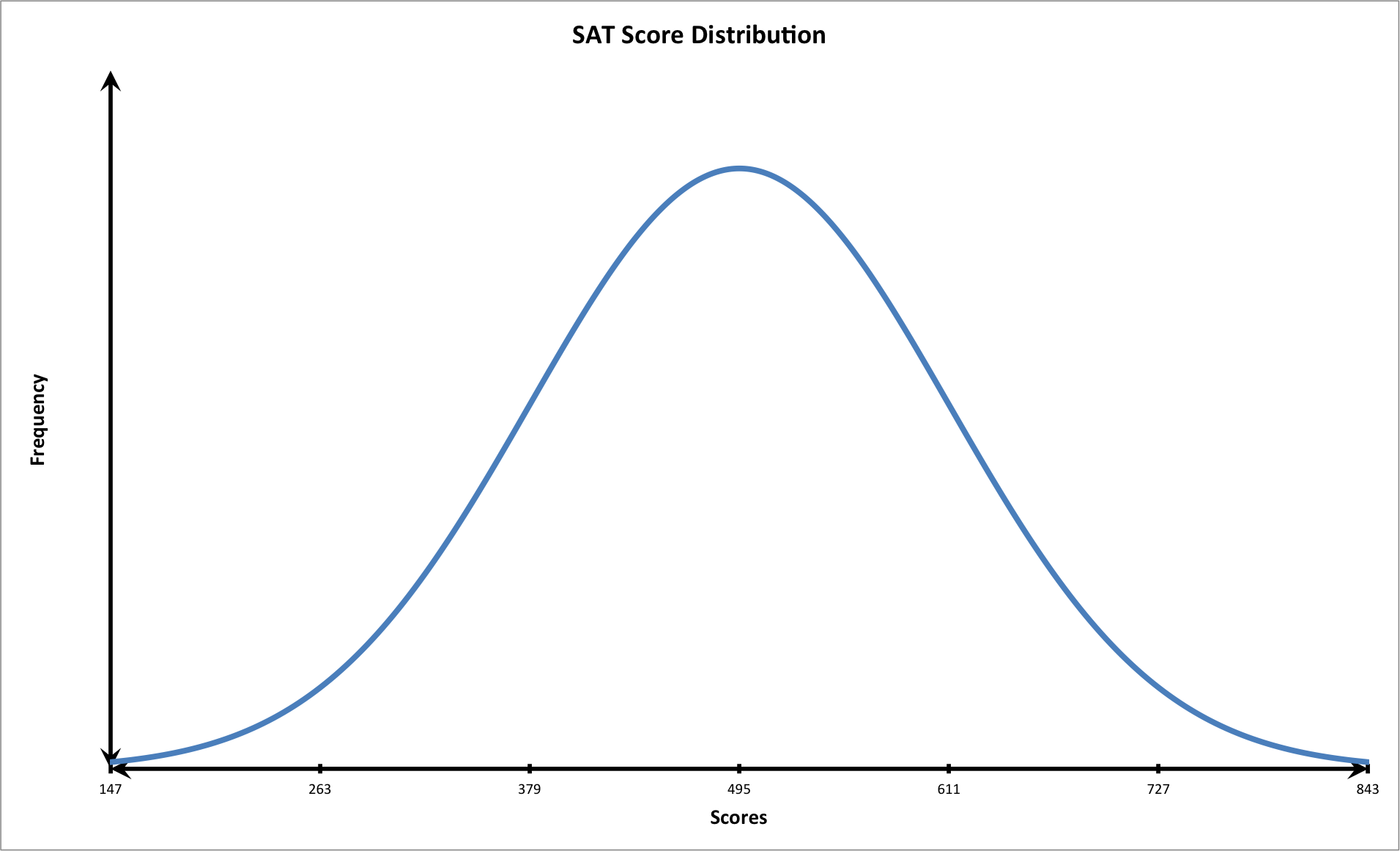
We know that the student had the following score:
Let's calculate two standard deviations above the mean.
The student scored very well: above two standard deviations from the mean. Notice that at this point on the graph, the tail of the curve is closer to the horizontal or x-axis. This means that fewer students scored this high on the exam. In other words, the student performed very well.
Example Question #4 : Fitting Data Sets To Normal Distribution And Estimating Area Under The Curve: Ccss.Math.Content.Hss Id.A.4
A social scientist performs an experiment testing the frequency and correlation of several demographics. She plots a histogram measuring income versus education level. She produces the following model:

Which of the following choices best describes this model?
Negative/left skewed distribution
Normal distribution
Uniform distribution
Positive/right skewed distribution
None of these
None of these
In order to solve this problem, let's review the following distributions: normal, positive/right skewed, negative/left skewed, bimodal, and uniform.
Normal Distribution:

A normal distribution is also known as a bell curve. Data that form a bell curve have three primary characteristics: the data is single peaked meaning that it has a single mode, it is symmetrical, and contains no outliers.
Positive/Right Skewed Distribution

A positive or right skewed distribution has a longer tail on the right side due to outliers while the majority of the points are concentrated on the left side of the graph. In other words, the set favors probabilities on the left of the model.
Negative/Left Skewed Distribution

A negative or left skewed distribution has a longer tail on the left side due to outliers while the majority of the points are concentrated on the right side of the graph. In other words, the set favors probabilities on the right of the model.
Bimodal Distribution

In a bimodal distribution, there are two peaks due to several modes in the data set. These multiple central tendencies are the result of two or more favorable probabilities in the set.
Uniform Distribution

In a uniform distribution, the data points form a a rectangle. These models are formed when data points possess a constant probability.
The model in the question does not match any of these; therefore, the correct answer is "none of these."
All Common Core: High School - Statistics and Probability Resources






































































































