In order to solve this problem, we need to discuss probabilities and more specifically conditional probabilities. We will start with discussing probabilities in a general sense. A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:

Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,

Now, let's convert this into a percentage:

Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur. 

Now that we understand the definition of a probability in its most general sense, we can investigate conditional probabilities. A conditional probability is defined as the probability that event B will occur given the information that an event A has already occurred.

It is expressed using the following equation:

In this equation, the probability of event B given that event A has occurred is equal to the probability of the intersection of events A and B divided by the probability of event A. It is important to note that if the events are independent, then the probability of event B given event A is simply the probability of event B because event A does not affect it.

Now, that we have an understanding of conditional probabilities let's investigate an example scenario. Let's use this information to calculate  in a Venn diagram.

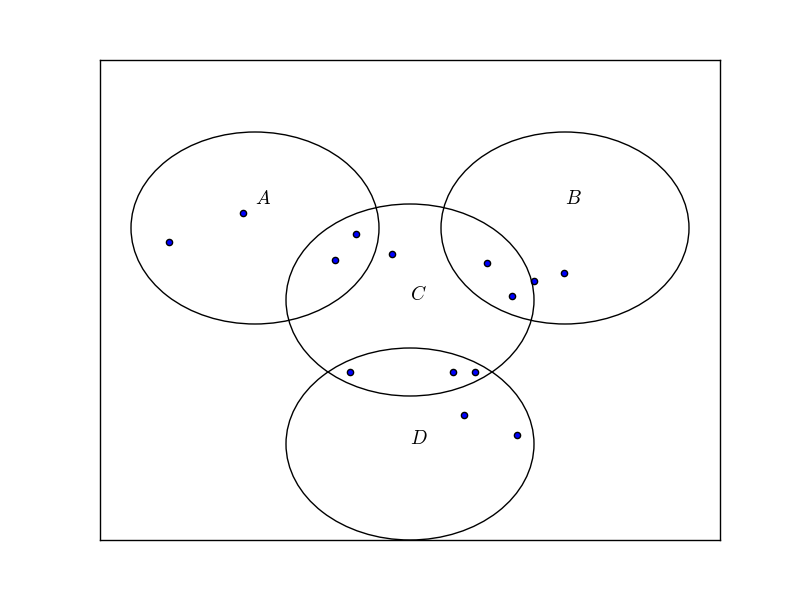
Given the information in the diagram and our knowledge of conditional probabilities we can derive the following equation:

Let's start by calculating the probability of the intersection of events A and C. In the digram there are  dots present in the area where circles A and C intersect; therefore, we can write the following:

Now, let's calculate the probability of event C. In the diagram we can see that circle C contains  dotes; therefore, we can write the following:

Now that we have calculated the two necessary probabilities we can substitute them into our conditional probability equation and solve.

Substitute.

Solve.

Now that we have worked through an example, let's investigate the scenario in the given question. First, lets derive an equation for the conditional probability:

Let's identify the probability for the intersection of events A and C.

Next, let's identify the probability of event C.

Substitute and solve.

Reduce.

In order to solve this problem, we need to discuss probabilities and more specifically conditional probabilities. We will start with discussing probabilities in a general sense. A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:

Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,

Now, let's convert this into a percentage:

Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur. 

Now that we understand the definition of a probability in its most general sense, we can investigate conditional probabilities. A conditional probability is defined as the probability that event B will occur given the information that an event A has already occurred.

It is expressed using the following equation:

In this equation, the probability of event B given that event A has occurred is equal to the probability of the intersection of events A and B divided by the probability of event A. It is important to note that if the events are independent, then the probability of event B given event A is simply the probability of event B because event A does not affect it.

Now, that we have an understanding of conditional probabilities let's investigate an example scenario. Let's use this information to calculate  in a Venn diagram.

Given the information in the diagram and our knowledge of conditional probabilities we can derive the following equation:

Let's start by calculating the probability of the intersection of events A and C. In the digram there are  dots present in the area where circles A and C intersect; therefore, we can write the following:

Now, let's calculate the probability of event C. In the diagram we can see that circle C contains  dotes; therefore, we can write the following:

Now that we have calculated the two necessary probabilities we can substitute them into our conditional probability equation and solve.

Substitute.

Solve.

Now that we have worked through an example, let's investigate the scenario in the given question. First, lets derive an equation for the conditional probability:

Let's identify the probability for the intersection of events A and C.

Next, let's identify the probability of event C.

Substitute and solve.