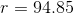All Common Core: High School - Geometry Resources
Example Questions
Example Question #1 : Cylinders, Pyramids, Cones, And Spheres Volume Formulas: Ccss.Math.Content.Hsg Gmd.A.3
Find the volume of a sphere, where the radius is 
Before we find the volume of a sphere, we need to recall the equation.
Since we are given the radius (
Thus the volume is,
Here is a picture representation of the sphere.

Example Question #1 : Cylinders, Pyramids, Cones, And Spheres Volume Formulas: Ccss.Math.Content.Hsg Gmd.A.3
Find the volume of a sphere, where the radius is 
Before we find the volume of a sphere, we need to recall the equation.
Since we are given the radius (
Thus the volume is,
Here is a picture representation of the sphere.

Example Question #37 : Geometric Measurement & Dimension
Find the volume of a sphere, where the radius is 
Before we find the volume of a sphere, we need to recall the equation.
Since we are given the radius (
Thus the volume is,
Here is a picture representation of the sphere.

Example Question #38 : Geometric Measurement & Dimension
Find the volume of a sphere, where the radius is 
Before we find the volume of a sphere, we need to recall the equation.
Since we are given the radius (
Thus the volume is,
Here is a picture representation of the sphere.

Example Question #1 : Cylinders, Pyramids, Cones, And Spheres Volume Formulas: Ccss.Math.Content.Hsg Gmd.A.3
Find the radius of a sphere, where the volume is 

Before we find the radius of a sphere, we need to recall the equation.
Since we are given the volume (
Now we can solve for 
Now we divide by
Now our equation is
To solve for 
Here is a picture representation of our sphere.

Example Question #2 : Cylinders, Pyramids, Cones, And Spheres Volume Formulas: Ccss.Math.Content.Hsg Gmd.A.3
Find the radius of a hemisphere, where the volume is 
Round your answer to 
Before we find the radius of a hemisphere, we need to recall the equation.
Since we are given the volume (
Now we can solve for 
Now we divide by
Now our equation is
To solve for 
Here is a picture of the hemisphere.

Example Question #2 : Cylinders, Pyramids, Cones, And Spheres Volume Formulas: Ccss.Math.Content.Hsg Gmd.A.3
Find the radius of a hemisphere, where the volume is
Round your answer to 
Before we find the radius of a hemisphere, we need to recall the equation.
Since we are given the volume (
Now we can solve for 
Now we divide by
Now our equation is
To solve for 
Here is a picture representation of the hemisphere.

Example Question #4 : Cylinders, Pyramids, Cones, And Spheres Volume Formulas: Ccss.Math.Content.Hsg Gmd.A.3
Find the radius of a hemisphere, where the volume is 
Round your answer to 
Before we find the radius of a hemisphere, we need to recall the equation.
Since we are given the volume (
Now we can solve for 
Now we divide by 
Now our equation is
To solve for 
Here is a picture of what the hemisphere look like.

Example Question #2 : Cylinders, Pyramids, Cones, And Spheres Volume Formulas: Ccss.Math.Content.Hsg Gmd.A.3
Find the radius of a hemisphere, where the volume is 
Round your answer to 
Before we find the radius of a hemisphere, we need to recall the equation.
Since we are given the volume (
Now we can solve for 
Now we divide by 
Now our equation is
To solve for 
Here is a picture of the hemisphere.

Example Question #1 : Cylinders, Pyramids, Cones, And Spheres Volume Formulas: Ccss.Math.Content.Hsg Gmd.A.3
Find the radius of a sphere, where the volume is 
Round your answer to 
Before we find the radius of a sphere, we need to recall the equation.
Since we are given the volume (
Now we can solve for 
Now we divide by 
Now our equation is
To solve for 
Here is a picture of the sphere.

Certified Tutor
Certified Tutor
All Common Core: High School - Geometry Resources