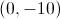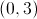All Common Core: 8th Grade Math Resources
Example Questions
Example Question #9 : How To Find X Or Y Intercept
Give the 


First, find the slope of the line, using the slope formula
setting 
By the point-slope formula, this line has the equation
where

or
To find the 


The 

Example Question #135 : Grade 8
Give the 


By the point-slope formula, this line has the equation
where
By substitution, the equation becomes

To find the 


The 

Example Question #11 : How To Find X Or Y Intercept
Find the y-intercept:
Rewrite the equation in slope-intercept form, 
The y-intercept is 

Example Question #314 : Geometry
What is the 
The graph has no 
The 




The 

Example Question #6 : How To Find Slope
What is the slope of the line with the equation
To find the slope, put the equation in the form of 
Since 
Example Question #11 : Use Similar Triangles To Show Equal Slopes: Ccss.Math.Content.8.Ee.B.6
Using the similar triangles, find the equation of the line in the provided graph.

The equation for a line can be written in the slope-intercept form:

In this equation, the variables 


One way to find the slope of a line is to solve for the rise over run:
This is defined as the change in the y-axis over the change in the x axis.
The triangles in the graph provide possess two different values for their respective rise over run calculations; however, both triangles should have the same slope:
Now that we've found the slope of our line, 
Therefore, the equation of this line is,
Example Question #142 : Grade 8
Using the similar triangles, find the equation of the line in the provided graph.

The equation for a line can be written in the slope-intercept form:

In this equation, the variables 


One way to find the slope of a line is to solve for the rise over run:
This is defined as the change in the y-axis over the change in the x axis.
The triangles in the graph provide possess two different values for their respective rise over run calculations; however, both triangle should have the same slope:
Now that we've found the slope of our line, 
Therefore, the equation of this line is,
Example Question #143 : Grade 8
Using the similar triangles, find the equation of the line in the provided graph.

The equation for a line can be written in the slope-intercept form:

In this equation, the variables 


One way to find the slope of a line is to solve for the rise over run:
This is defined as the change in the y-axis over the change in the x axis.
The triangles in the graph provide possess two different values for their respective rise over run calculations; however, both triangle should have the same slope:
Now that we've found the slope of our line, 
Therefore, the equation of this line is,
Example Question #144 : Grade 8
Using the similar triangles, find the equation of the line in the provided graph.

The equation for a line can be written in the slope-intercept form:

In this equation, the variables 


One way to find the slope of a line is to solve for the rise over run:
This is defined as the change in the y-axis over the change in the x axis.
The triangles in the graph provide possess two different values for their respective rise over run calculations; however, both triangle should have the same slope:
Now that we've found the slope of our line, 
Therefore, the equation of this line is,
Example Question #145 : Grade 8
Using the similar triangles, find the equation of the line in the provided graph.

The equation for a line can be written in the slope-intercept form:

In this equation, the variables 


One way to find the slope of a line is to solve for the rise over run:
This is defined as the change in the y-axis over the change in the x axis.
The triangles in the graph provide possess two different values for their respective rise over run calculations; however, both triangle should have the same slope:
Now that we've found the slope of our line, 
Therefore, the equation of this line is,
All Common Core: 8th Grade Math Resources