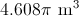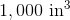Call Now to Set Up Tutoring:

(888) 888-0446

Common Core: 8th Grade Math : Know and Use the Formulas for the Volumes of Cones, Cylinders, and Spheres: CCSS.Math.Content.8.G.C.9

Study concepts, example questions & explanations for Common Core: 8th Grade Math

Create An Account

All Common Core: 8th Grade Math Resources

7 Diagnostic Tests 75 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #101 : Solid Geometry

A cone has height 240 centimeters; its base has radius 80 centimeters. Give its volume in cubic meters.

Possible Answers:

$0.768 \pi \textrm{ m}^{3}$

$1.536 \pi \textrm{ m}^{3}$

$0.512 \pi \textrm{ m}^{3}$

$4.608 \pi \textrm{ m}^{3}$

Correct answer:

$0.512 \pi \textrm{ m}^{3}$

Explanation:

Convert both dimensions from centimeters to meters by dividing by 100:

Height: 240 centimeters = $240 \div 100 = 2.4$ meters.

Radius: 80 centimeters = $80 \div 100 = 0.8$ meters.

Substitute r = 0.8, h = 2.4 in the volume formula:

$V = \frac{1}{3} \pi r^{2}h$

$V = \frac{1}{3} \cdot \pi \cdot 0.8 ^{2} \cdot 2.4$

$V = \frac{1}{3}\cdot 0.8 \cdot 0.8 \cdot 2.4 \cdot \pi$

$V =0.512 \pi$

Report an Error

Example Question #1 : How To Find The Volume Of A Cone

Give the volume of a cone whose height is 10 inches and whose base is a circle with circumference $6 \pi$ inches.

Possible Answers:

$30 \pi \textrm{ in}^{3}$

$45 \pi \textrm{ in}^{3}$

$120 \pi \textrm{ in}^{3}$

$360 \pi \textrm{ in}^{3}$

$90 \pi \textrm{ in}^{3}$

Correct answer:

$30 \pi \textrm{ in}^{3}$

Explanation:

A circle with circumference $6 \pi$ inches has as its radius

$r = \frac{C }{2\pi }=\frac{6\pi }{2\pi } = 3$ inches.

The area of the base is therefore

$B = \pi r^{2} = \pi \cdot 3^{2} = 9 \pi$ square inches.

To find the volume of the cone, substitute $B = 9 \pi , h = 10$ in the formula for the volume of a cone:

$V = \frac{1}{3} Bh = \frac{1}{3} \cdot 9 \pi \cdot 10 = 30 \pi$ cubic inches

Report an Error

Example Question #501 : Grade 8

The height of a cone and the radius of its base are equal. The circumference of the base is $10 \pi$ inches. Give its volume.

Possible Answers:

$\frac{5,000}{3} \pi \textrm{ in}^{3}$

$1,000 \textrm{ in}^{3}$

$\frac{125}{3} \pi \textrm{ in}^{3}$

$\frac{1,000}{3} \pi \textrm{ in}^{3}$

$125 \textrm{ in}^{3}$

Correct answer:

$\frac{125}{3} \pi \textrm{ in}^{3}$

Explanation:

A circle with circumference $10 \pi$ inches has as its radius

$r = \frac{C }{2\pi }=\frac{10\pi }{2\pi } = 5$ inches.

The height is also inches, so substitute h = r = 5 in the volume formula for a cone:

$V = \frac{1}{3} \pi r ^{2}h = \frac{1}{3} \pi \cdot 5 ^{2} \cdot 5 = \frac{125}{3} \pi$ cubic inches

Report an Error

Example Question #1 : Volume Of A Sphere

In terms of $\pi$ , give the volume, in cubic inches, of a spherical water tank with a diameter of 20 feet.

Possible Answers:

$230,400 \pi\textrm{ in}^{3}$

$2,304,000 \pi \textrm{ in}^{3}$

$18,432,000\pi\textrm{ in}^{3}$

$307,200\pi\textrm{ in}^{3}$

$57,600 \pi\textrm{ in}^{3}$

Correct answer:

$2,304,000 \pi \textrm{ in}^{3}$

Explanation:

20 feet = $20 \times 12 = 240$ inches, the diameter of the tank; half of this, or 120 inches, is the radius. Set r = 120 , substitute in the volume formula, and solve for :

$V = \frac{4}{3} \pi r^{3}$

$V = \frac{4}{3} \pi \cdot 120^{3}$

$V = \frac{4}{3} \pi \cdot 1,728,000$

$V = 2,304,000 \pi$ cubic inches

Report an Error

Example Question #71 : Solid Geometry

A sphere has diameter 3 meters. Give its volume in cubic centimeters (leave in terms of $\pi$ ).

Possible Answers:

$36,000,000\pi \textrm{ cm}^{3}$

$1,125,000\pi \textrm{ cm}^{3}$

$4,500,000\pi \textrm{ cm}^{3}$

$3,375,000\pi \textrm{ cm}^{3}$

$27,000,000\pi \textrm{ cm}^{3}$

Correct answer:

$4,500,000\pi \textrm{ cm}^{3}$

Explanation:

The diameter of 3 meters is equal to $3 \times 100 = 300$ centimeters; the radius is half this, or 150 centimeters. Substitute r = 150 in the volume formula:

$V= \frac{4}{3} \pi r^{3}$

$V= \frac{4}{3} \cdot \pi \cdot 150^{3}$

$V= \frac{4}{3} \cdot 150 \cdot 150 \cdot 150\cdot \pi$

$V= 4,500,000\pi$ cubic centimeters

Report an Error

Example Question #11 : Volume Of A Three Dimensional Figure

A cone has a radius of inches and a height of inches. Find the volume of the cone.

Possible Answers:

$12\pi\:in^3$

$24\pi\:in^3$

$36\pi\:in^3$

$108\pi\:in^3$

Correct answer:

$36\pi\:in^3$

Explanation:

The volume of a cone is given by the formula:

$\text{Volume}=\frac{1}{3}\pi r^2h$

Now, plug in the values of the radius and height to find the volume of the given cone.

$\text{Volume}=\frac{1}{3}\pi\times3^2\times12=\frac{1}{3}\pi\times9\times12=\frac{108}{3}\pi=36\pi\:in^3$

Report an Error

Example Question #23 : Know And Use The Formulas For The Volumes Of Cones, Cylinders, And Spheres: Ccss.Math.Content.8.G.C.9

Calculate the volume of the cylinder provided. Round the answer to the nearest hundredth.

Possible Answers:

$907.45\textup{ in}^3$

$924.84\textup{ in}^3$

$933.24\textup{ in}^3$

$913.33\textup{ in}^3$

$904.78\textup{ in}^3$

Correct answer:

$904.78\textup{ in}^3$

Explanation:

In order to solve this problem, we need to recall the formula used to calculate the volume of a cylinder:

$V=\pi r^2h$

Now that we have this formula, we can substitute in the given values and solve:

$V=\pi6^2(8)$

$V=\pi36(8)$

$V=\pi288$

$V=904.78\textup{ in}^3$

Report an Error

Example Question #191 : Geometry

Calculate the volume of the cone provided. Round the answer to the nearest hundredth.

Possible Answers:

$320.14\textup{ in}^3$

$314.16\textup{ in}^3$

$364.16\textup{ in}^3$

$315\textup{ in}^3$

$300\textup{ in}^3$

Correct answer:

$314.16\textup{ in}^3$

Explanation:

In order to solve this problem, we need to recall the formula used to calculate the volume of a cone:

$V=\pi r^2\left ( \frac{h}{3} \right )$

Now that we have this formula, we can substitute in the given values and solve:

$V=\pi5^2\left ( \frac{12}{3} \right )$

$V=\pi25(4)$

$V=\pi100$

$V=314.16\textup{ in}^3$

Report an Error

Example Question #192 : Geometry

Calculate the volume of the cone provided. Round the answer to the nearest hundredth.

Possible Answers:

$160.21\textup{ in}^3$

$142.80\textup{ in}^3$

$150.80\textup{ in}^3$

$155.32\textup{ in}^3$

$162.38\textup{ in}^3$

Correct answer:

$150.80\textup{ in}^3$

Explanation:

In order to solve this problem, we need to recall the formula used to calculate the volume of a cone:

$V=\pi r^2\left ( \frac{h}{3} \right )$

Now that we have this formula, we can substitute in the given values and solve:

$V=\pi4^2\left ( \frac{9}{3} \right )$

$V=\pi16(3)$

$V=\pi48$

$V=150.80\textup{ in}^3$

Report an Error

Example Question #21 : Know And Use The Formulas For The Volumes Of Cones, Cylinders, And Spheres: Ccss.Math.Content.8.G.C.9

Calculate the volume of the cone provided. Round the answer to the nearest hundredth.

Possible Answers:

$62.22\textup{ in}^3$

$64.62\textup{ in}^3$

$58.45\textup{ in}^3$

$56.55\textup{ in}^3$

$60.23\textup{ in}^3$

Correct answer:

$56.55\textup{ in}^3$

Explanation:

In order to solve this problem, we need to recall the formula used to calculate the volume of a cone:

$V=\pi r^2\left ( \frac{h}{3} \right )$

Now that we have this formula, we can substitute in the given values and solve:

$V=\pi3^2\left ( \frac{6}{3} \right )$

$V=\pi9(2)$

$V=\pi18$

$V=56.55\textup{ in}^3$

Report an Error

View Tutors

Ingy
Certified Tutor

University of Minnesota-Twin Cities, Bachelors, Mathematics with Actuarial Science Specialization.

View Tutors

Sarah
Certified Tutor

New York University, Bachelor of Fine Arts, Drama.

View Tutors

Justin
Certified Tutor

University of Toledo, Bachelors, Environmental Science. University of Michigan, Masters, Natural Resource Management.

All Common Core: 8th Grade Math Resources

7 Diagnostic Tests 75 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Spanish Tutors in Miami, MCAT Tutors in Philadelphia, SAT Tutors in Washington DC, LSAT Tutors in Chicago, ACT Tutors in Atlanta, GRE Tutors in Phoenix, Reading Tutors in Houston, Reading Tutors in New York City, Statistics Tutors in Atlanta, Reading Tutors in San Diego

Popular Courses & Classes

MCAT Courses & Classes in New York City, Spanish Courses & Classes in Miami, SSAT Courses & Classes in New York City, GMAT Courses & Classes in Dallas Fort Worth, GRE Courses & Classes in San Diego, ISEE Courses & Classes in San Francisco-Bay Area, MCAT Courses & Classes in Phoenix, LSAT Courses & Classes in Phoenix, SSAT Courses & Classes in Philadelphia, MCAT Courses & Classes in San Francisco-Bay Area

Popular Test Prep

ACT Test Prep in Chicago, ISEE Test Prep in Denver, GRE Test Prep in Houston, ACT Test Prep in New York City, GRE Test Prep in Los Angeles, LSAT Test Prep in New York City, LSAT Test Prep in Boston, LSAT Test Prep in Philadelphia, LSAT Test Prep in Houston, SSAT Test Prep in Boston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Common Core: 8th Grade Math : Know and Use the Formulas for the Volumes of Cones, Cylinders, and Spheres: CCSS.Math.Content.8.G.C.9

Study concepts, example questions & explanations for Common Core: 8th Grade Math

All Common Core: 8th Grade Math Resources

Example Questions

Example Question #101 : Solid Geometry

Example Question #1 : How To Find The Volume Of A Cone

Example Question #501 : Grade 8

Example Question #1 : Volume Of A Sphere

Example Question #71 : Solid Geometry

Example Question #11 : Volume Of A Three Dimensional Figure

Example Question #23 : Know And Use The Formulas For The Volumes Of Cones, Cylinders, And Spheres: Ccss.Math.Content.8.G.C.9

Example Question #191 : Geometry

Example Question #192 : Geometry

Example Question #21 : Know And Use The Formulas For The Volumes Of Cones, Cylinders, And Spheres: Ccss.Math.Content.8.G.C.9

All Common Core: 8th Grade Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: