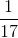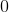All Common Core: 7th Grade Math Resources
Example Questions
Example Question #851 : Grade 7
Joe has a bag of 



Joe starts out with 

Now that Joe has taken a red marble from the bag, we still have 

Example Question #852 : Grade 7
Dan has a bag of 





Dan starts out with 

Now that Dan has taken a purple marble from the bag, we still have 

Example Question #853 : Grade 7
Joe has a bag of 



Joe starts out with 

Now that Joe has taken a red marble from the bag, we have only 

Example Question #851 : Grade 7
Joe has a bag of 



Joe starts out with 

Now that Joe has taken a yellow marble from the bag, we have only 

Example Question #852 : Grade 7
Joe has a bag of 



Joe starts out with 

Now that Joe has taken a blue marble from the bag, we have only 

Example Question #852 : Grade 7
Joe has a bag of 



Joe starts out with 

Now that Joe has taken a red marble from the bag, we still have 

Example Question #854 : Grade 7
Dan has a bag of 





Dan starts out with 

Now that Dan has taken a red marble from the bag, we still have 

Example Question #861 : Grade 7
Dan has a bag of 





Dan starts out with 

Now that Dan has taken a yellow marble from the bag, we still have 

Example Question #4 : Understand Fraction Of Outcomes: Ccss.Math.Content.7.Sp.C.8a
Dan has a bag of 





Dan starts out with 

Now that Dan has taken an orange marble from the bag, we still have 

Example Question #5 : Understand Fraction Of Outcomes: Ccss.Math.Content.7.Sp.C.8a
Dan has a bag of 





Dan starts out with 

Now that Dan has taken an orange marble from the bag, we have 

All Common Core: 7th Grade Math Resources