\(\displaystyle F = \frac{9}{5} C + 32\)

\(\displaystyle F = \frac{9}{5} \cdot 65 + 32 = 117+32 = 149 ^{\circ } F\)

\(\displaystyle C = \frac{5}{9} (F-32)\)

\(\displaystyle C = \frac{5}{9} (80-32)\)

\(\displaystyle C = \frac{5}{9} \cdot 48 \approx 26.7\), which rounds to \(\displaystyle 27^{\circ } C\)

If there are 500 apples and 1 in 50 will remain unharvested, then we can find the number of unharvested apples by multiplying. 

\(\displaystyle 500\times \frac{1}{50}=10\)

10 apples will remain unharvested. Of those, half will rot on the ground. Multiply to find how many apples rot on the ground.

\(\displaystyle 10\times\frac{1}{2}=5\)

5 apples will rot on the ground.

This problem involves two seperate multiplication problems. Erin will make $450 at the reunion but supplies cost her $300 to make the shirts. So her profit is $150.

Let \(\displaystyle x\) represent the unknown quantity.

The first expression:

"The product of a number and three" is three times this number, or 

\(\displaystyle 3x\)

"Ten added to the product" is

\(\displaystyle 3x+10\)

The second expression:

"Twice the number" is two times the number, or

\(\displaystyle 2x\).

The desired equation is therefore

\(\displaystyle 3x+ 10 = 2x\).

"The difference of a number and nine" is the result of a subtraction of the two, so we write this as

\(\displaystyle y- 9\)

"Five-sevenths of" this difference is the product of \(\displaystyle \frac{5}{7}\) and this, or

\(\displaystyle \frac{5}{7} (y- 9)\)

This is equal to forty, so write the equation as

\(\displaystyle \frac{5}{7} (y- 9) = 40\)

Let \(\displaystyle x\) represent the unknown number.

"The sum of a number and ten" is the expression \(\displaystyle x+ 10\). "Twice" this sum is two times this expression, or

\(\displaystyle 2 (x+10)\).

"The difference of the number and one half" is a subtraction of the two, or

\(\displaystyle x - \frac{1}{2}\)

Set these equal, and the desired equation is

\(\displaystyle 2 (x+10) = x - \frac{1}{2}\)

In ten years, Mark will be \(\displaystyle 43\) years old, so Mark is \(\displaystyle 43-10 = 33\) years old now, and Brian is one-third of this, or \(\displaystyle 33 \div 3 = 11\) years old. 

Let \(\displaystyle N\) be the number of years in which Mark will be twice Brian's age. Then Brian will be \(\displaystyle N + 11\), and Mark will be \(\displaystyle N + 33\). Since Mark will be twice Brian's age, we can set up and solve the equation:

\(\displaystyle 2 (N + 11) = N + 33\)

\(\displaystyle 2N + 22 = N + 33\)

\(\displaystyle 2N + 22-N - 22 = N + 33 -N - 22\)

\(\displaystyle N = 11\)

Mark will be twice Brian's age in \(\displaystyle 11\) years.

Since Gary will be 37 in five years, he is \(\displaystyle 37 - 5 = 32\) years old now. He is twice as old as Cathy, so she is \(\displaystyle 32 \div 2 =16\) years old, and in five years, she will be \(\displaystyle 16 + 5 = 21\) years old.

In order to solve this problem, we need to recall the formula for perimeter of a rectangle:

\(\displaystyle P=2l+2w\)

We can substitute in our known values and solve for our unknown variable (i.e. length):

\(\displaystyle 18=2l+2(2)\)

\(\displaystyle 18=2l+4\)

We want to isolate the \(\displaystyle l\) to one side of the equation. In order to do this, we will first subtract \(\displaystyle 4\) from both sides of the equation. 

\(\displaystyle \frac{\begin{array}[b]{r}18=2l+4\\ -4\ \ \ \ \ \ -4\end{array}}{\\\\14=2l}\)

Next, we can divide each side by \(\displaystyle 2\)

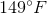
\(\displaystyle \frac{\begin{array}[b]{r}\frac{14}{2}=\frac{2l}{2}\\\end{array}}{7=l}\)

The length of the rectangle is \(\displaystyle 7\textup{ inches}\)