Call Now to Set Up Tutoring:

(888) 888-0446

Common Core: 7th Grade Math : Solve Simple Equations for an Unknown Angle in a Figure: CCSS.Math.Content.7.G.B.5

Study concepts, example questions & explanations for Common Core: 7th Grade Math

Create An Account

All Common Core: 7th Grade Math Resources

7 Diagnostic Tests 110 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Solve Simple Equations For An Unknown Angle In A Figure: Ccss.Math.Content.7.G.B.5

One angle of an isosceles triangle has measure $110^{\circ }$ . What are the measures of the other two angles?

Possible Answers:

Not enough information is given to answer this question.

$45^{\circ }, 45^{\circ }$

$35^{\circ },35^{\circ }$

$110 ^{\circ }, 40 ^{\circ }$

$70^{\circ }, 70^{\circ }$

Correct answer:

$35^{\circ },35^{\circ }$

Explanation:

An isosceles triangle not only has two sides of equal measure, it has two angles of equal measure. This means one of two things, which we examine separately:

Case 1: It has another $110^{\circ }$ angle. This is impossible, since a triangle cannot have two obtuse angles.

Case 2: Its other two angles are the ones that are of equal measure. If we let be their common measure, then, since the sum of the measures of a triangle is $180^{\circ }$ ,

x + x + 110 = 180

2x + 110 = 180

2x + 110 -110= 180 -110

2x= 70

$2x \div 2= 70 \div 2$

x = 35

Both angles measure $35^{\circ}$

Report an Error

Example Question #2 : How To Find The Measure Of An Angle

Two angles are supplementary and have a ratio of 1:4. What is the size of the smaller angle?

Possible Answers:

$144^{\circ}$

$45^{\circ}$

$36^{\circ}$

$18^{\circ}$

$72^{\circ}$

Correct answer:

$36^{\circ}$

Explanation:

Since the angles are supplementary, their sum is 180 degrees. Because they are in a ratio of 1:4, the following expression could be written:

$x+4x=180$

$5x=180$

$x=36^{\circ}$

Report an Error

Example Question #6 : How To Find The Measure Of An Angle

What angle is complementary to $65$^{\circ}$$ ?

Possible Answers:

$130$^{\circ}$$

$25$^{\circ}$$

$115$^{\circ}$$

$65$^{\circ}$$

$35$^{\circ}$$

Correct answer:

$25$^{\circ}$$

Explanation:

To find the other angle, subtract the given angle from $90$^{\circ}$$ since complementary angles add up to $90$^{\circ}$$ .

The complementary is:

$\angle 90-\angle65 = \angle25$

Report an Error

Example Question #11 : How To Find The Measure Of An Angle

What is the supplementary angle to $100$^{\circ}$$ ?

Possible Answers:

$170$^{\circ}$$

$10$^{\circ}$$

$280$^{\circ}$$

$70$^{\circ}$$

$80$^{\circ}$$

Correct answer:

$80$^{\circ}$$

Explanation:

Supplementary angles add up to $180$^{\circ}$$ . In order to find the correct angle, take the known angle and subtract that from $180$^{\circ}$$ .

$180$^{\circ}$ -100$^{\circ}$ = 80$^{\circ}$$

Report an Error

Example Question #1 : Solve Simple Equations For An Unknown Angle In A Figure: Ccss.Math.Content.7.G.B.5

What angle is complement to $\frac{\pi}{6}$ ?

Possible Answers:

$\frac{\pi}{3}$

$\frac{\pi}{4}$

$\frac{2\pi}{3}$

$\frac{\pi}{6}$

$\frac{\pi}{9}$

Correct answer:

$\frac{\pi}{3}$

Explanation:

The complement to an angle is ninety degrees subtract the angle since two angles must add up to 90. In this case, since we are given the angle in radians, we are subtracting from $\frac{\pi}{2}$ instead to find the complement. The conversion between radians and degrees is: $\pi \textup{ radians } = 180 \textup{ degrees}$

$\frac{\pi}{2}-\frac{\pi}{6}$

Reconvert the fractions to the least common denominator.

$\frac{\pi}{2}-\frac{\pi}{6} = \frac{3\pi}{6}-\frac{\pi}{6} = \frac{2\pi}{6}$

Reduce the fraction.

$\frac{2\pi}{6} = \frac{\pi}{3}$

Report an Error

Example Question #91 : Plane Geometry

Exterior_angle

Note: Figure NOT drawn to scale.

What is the measure of angle

Possible Answers:

y = 124

y = 134

y = 152

y = 129

y = 142

Correct answer:

y = 124

Explanation:

The two angles at bottom are marked as congruent. One forms a linear pair with a $152 ^{\circ }$ angle, so it is supplementary to that angle, making its measure $(180-152)^{\circ } = 28^{\circ }$ . Therefore, each marked angle measures $28^{\circ }$ .

The sum of the measures of the interior angles of a triangle is $180^{\circ }$ , so:

y + 28 + 28 = 180

y +56= 180

y +56-56 = 180-56

y = 124

Report an Error

Example Question #3 : Triangles

One of the base angles of an isosceles triangle is $42^{\circ}$ . Give the measure of the vertex angle.

Possible Answers:

$86 ^{\circ}$

$98 ^{\circ}$

$96 ^{\circ}$

$100^{\circ}$

$90^{\circ}$

Correct answer:

$96 ^{\circ}$

Explanation:

The base angles of an isosceles triangle are always equal. Therefore both base angles are $42^{\circ}$ .

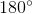
Let the measure of the third angle. Since the sum of the angles of a triangle is $180^{\circ}$ , we can solve accordingly:

$42+42+x=180\Rightarrow x=180-84\Rightarrow x=96^{\circ}$

Report an Error

Example Question #2 : Solve Simple Equations For An Unknown Angle In A Figure: Ccss.Math.Content.7.G.B.5

The figure represents a set of complementary angles, solve for .

Possible Answers:

$52^\circ$

$53^\circ$

$55^\circ$

$56^\circ$

$54^\circ$

Correct answer:

$56^\circ$

Explanation:

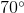
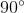
Complementary angles are defined as two angles that when added together equal $90^\circ$

From the question, we know that the two angles are complimentary, and thus equal $90^\circ$ , so we can set up the following equation:

x+34=90

Next we can solve for :

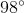
$\frac{\begin{array}[b]{r}x+34=90\\ -34-34\end{array}}{x= 56}$

Report an Error

Example Question #3 : Solve Simple Equations For An Unknown Angle In A Figure: Ccss.Math.Content.7.G.B.5

The figure represents a set of complementary angles, solve for .

Possible Answers:

$67^\circ$

$64^\circ$

$68^\circ$

$66^\circ$

$65^\circ$

Correct answer:

$65^\circ$

Explanation:

Complementary angles are defined as two angles that when added together equal $90^\circ$

From the question, we know that the two angles are complimentary, and thus equal $90^\circ$ , so we can set up the following equation:

x+25=90

Next we can solve for :

$\frac{\begin{array}[b]{r}x+25=90\\ -25-25\end{array}}{x= 65}$

Report an Error

Example Question #4 : Solve Simple Equations For An Unknown Angle In A Figure: Ccss.Math.Content.7.G.B.5

The figure represents a set of complementary angles, solve for .

Possible Answers:

$69^\circ$

$68^\circ$

$70^\circ$

$71^\circ$

$67^\circ$

Correct answer:

$70^\circ$

Explanation:

Complementary angles are defined as two angles that when added together equal $90^\circ$

From the question, we know that the two angles are complimentary, and thus equal $90^\circ$ , so we can set up the following equation:

x+20=90

Next we can solve for :

$\frac{\begin{array}[b]{r}x+20=90\\ -20-20\end{array}}{x= 70}$

Report an Error

View Tutors

Rainier
Certified Tutor

Norfolk State University, Bachelors, Physics.

View Tutors

Marlene
Certified Tutor

Herbert Lehman, Bachelors, Recreation Education. Long Island University-Brooklyn Campus, Masters, Special Education.

View Tutors

Sarah
Certified Tutor

New York University, Bachelor of Fine Arts, Drama.

All Common Core: 7th Grade Math Resources

7 Diagnostic Tests 110 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Algebra Tutors in Dallas Fort Worth, SAT Tutors in Denver, Statistics Tutors in Washington DC, Reading Tutors in Dallas Fort Worth, Math Tutors in Boston, SAT Tutors in Philadelphia, Math Tutors in Chicago, Reading Tutors in Houston, Spanish Tutors in Washington DC, French Tutors in Miami

Popular Courses & Classes

LSAT Courses & Classes in San Diego, ISEE Courses & Classes in New York City, SAT Courses & Classes in San Francisco-Bay Area, GMAT Courses & Classes in Washington DC, SAT Courses & Classes in Boston, ISEE Courses & Classes in Dallas Fort Worth, SSAT Courses & Classes in Atlanta, ISEE Courses & Classes in Chicago, Spanish Courses & Classes in San Diego, GMAT Courses & Classes in Seattle

Popular Test Prep

ISEE Test Prep in Seattle, ISEE Test Prep in Denver, ACT Test Prep in Miami, GMAT Test Prep in Seattle, GRE Test Prep in Philadelphia, GRE Test Prep in San Francisco-Bay Area, GRE Test Prep in Houston, GRE Test Prep in Washington DC, GMAT Test Prep in Denver, SSAT Test Prep in Chicago

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Common Core: 7th Grade Math : Solve Simple Equations for an Unknown Angle in a Figure: CCSS.Math.Content.7.G.B.5

Study concepts, example questions & explanations for Common Core: 7th Grade Math

All Common Core: 7th Grade Math Resources

Example Questions

Example Question #1 : Solve Simple Equations For An Unknown Angle In A Figure: Ccss.Math.Content.7.G.B.5

Example Question #2 : How To Find The Measure Of An Angle

Example Question #6 : How To Find The Measure Of An Angle

Example Question #11 : How To Find The Measure Of An Angle

Example Question #1 : Solve Simple Equations For An Unknown Angle In A Figure: Ccss.Math.Content.7.G.B.5

Example Question #91 : Plane Geometry

Example Question #3 : Triangles

Example Question #2 : Solve Simple Equations For An Unknown Angle In A Figure: Ccss.Math.Content.7.G.B.5

Example Question #3 : Solve Simple Equations For An Unknown Angle In A Figure: Ccss.Math.Content.7.G.B.5

Example Question #4 : Solve Simple Equations For An Unknown Angle In A Figure: Ccss.Math.Content.7.G.B.5

All Common Core: 7th Grade Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: