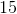All Common Core: 7th Grade Math Resources
Example Questions
Example Question #1 : Solve Problems With The Four Operations With Rational Numbers: Ccss.Math.Content.7.Ns.A.3
Solve:
Example Question #2 : Solve Problems With The Four Operations With Rational Numbers: Ccss.Math.Content.7.Ns.A.3
Remember PEMDAS. The parentheses comes first. When adding a negative value, the operation is subtraction. We now have 


Example Question #3 : Solve Problems With The Four Operations With Rational Numbers: Ccss.Math.Content.7.Ns.A.3
When given multiple operations, remember PEMDAS. Division comes before subtraction. So we divide 










Example Question #4 : Solve Problems With The Four Operations With Rational Numbers: Ccss.Math.Content.7.Ns.A.3
Remember PEMDAS. The parentheses comes first so let's work what's inside. When adding a negative sign, the operation becomes negative. So, we have 







Example Question #5 : Solve Problems With The Four Operations With Rational Numbers: Ccss.Math.Content.7.Ns.A.3
Remember PEMDAS. Let's work the parantheses first. For 






















Example Question #6 : Solve Problems With The Four Operations With Rational Numbers: Ccss.Math.Content.7.Ns.A.3
Remember PEMDAS. The parantheses come first. On the left we have 











Example Question #7 : Solve Problems With The Four Operations With Rational Numbers: Ccss.Math.Content.7.Ns.A.3
We need to take care of the parentheses first because of PEMDAS. Parentheses has priority over everything. The product is 

Example Question #8 : Solve Problems With The Four Operations With Rational Numbers: Ccss.Math.Content.7.Ns.A.3
Remember PEMDAS. Parentheses comes first then multiplication. 


Example Question #9 : Solve Problems With The Four Operations With Rational Numbers: Ccss.Math.Content.7.Ns.A.3
Remember PEMDAS. Parenthesis comes first then multiplication. 




Example Question #5 : Solve Problems With The Four Operations With Rational Numbers: Ccss.Math.Content.7.Ns.A.3
Solve:
We know the following information:
In this particular case, do the negative numbers change our answer? There are a couple of rules that we need to remember when multiplying with negative numbers to help us answer this question:
- A negative number multiplied by a positive number will always equal a negative number
- A negative number multiplied by a negative number will always equal a positive number
Thus,
All Common Core: 7th Grade Math Resources