All Common Core: 7th Grade Math Resources
Example Questions
Example Question #181 : Ratios & Proportional Relationships
A sweater was originally 

In order to solve this problem, we need to calculate 

We can convert a percent into a decimal by moving the decimal two places to the left:
Next, we can multiply:
Remember, we are taking 
Example Question #181 : Grade 7
A sweater was originally 

In order to solve this problem, we need to calculate 

We can convert a percent into a decimal by moving the decimal two places to the left:
Next, we can multiply:
Remember, we are taking 
Example Question #181 : Grade 7
A sweater was originally 

In order to solve this problem, we need to calculate 

We can convert a percent into a decimal by moving the decimal two places to the left:
Next, we can multiply:
Remember, we are taking 
Example Question #183 : Ratios & Proportional Relationships
A sweater was originally 

In order to solve this problem, we need to calculate 

We can convert a percent into a decimal by moving the decimal two places to the left:
Next, we can multiply:
Remember, we are taking 
Example Question #182 : Ratios & Proportional Relationships
A sweater was originally 

In order to solve this problem, we need to calculate 

We can convert a percent into a decimal by moving the decimal two places to the left:
Next, we can multiply:
Remember, we are taking 
Example Question #182 : Grade 7
A sweater was originally 

In order to solve this problem, we need to calculate 

We can convert a percent into a decimal by moving the decimal two places to the left:
Next, we can multiply:
Remember, we are taking 
Example Question #182 : Grade 7
A sweater was originally 

In order to solve this problem, we need to calculate 

We can convert a percent into a decimal by moving the decimal two places to the left:
Next, we can multiply:
Remember, we are taking 
Example Question #183 : Grade 7
A sweater was originally 

In order to solve this problem, we need to calculate 

We can convert a percent into a decimal by moving the decimal two places to the left:
Next, we can multiply:
Remember, we are taking 
Example Question #1 : The Number System
Compute the following:
Convert all the double signs to a single sign before solving. Remember, two minus (negative) signs combine to form a plus (positive) sign, and a plus (positive) sign and a minus (negative) sign combine to form a minus (negative) sign.
Example Question #2 : Describe Situations In Which Opposite Quantities Combine To Make 0: Ccss.Math.Content.7.Ns.A.1a
For the equation provided, what value when substituted for 
In order to answer this question, we can solve for 


We can subtract 

Certified Tutor
Certified Tutor
All Common Core: 7th Grade Math Resources







![\frac{\begin{array}[b]{r}38\\ \times\ .10\end{array}}{ \ \ \ \space 3.80}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/912698/gif.latex)
![\frac{\begin{array}[b]{r}38.00\\ -\ 3.80\end{array}}{ \ \ \space 34.20}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/912700/gif.latex)






![\frac{\begin{array}[b]{r}27\\ \times\ .10\end{array}}{ \ \ \ \space 2.70}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/912712/gif.latex)
![\frac{\begin{array}[b]{r}27.00\\ -\ 2.70\end{array}}{ \ \ \space 24.30}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/912714/gif.latex)






![\frac{\begin{array}[b]{r}14\\ \times\ .10\end{array}}{ \ \ \ \space 1.40}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/912725/gif.latex)
![\frac{\begin{array}[b]{r}14.00\\ -\ 1.40\end{array}}{ \ \ \space 12.60}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/912727/gif.latex)






![\frac{\begin{array}[b]{r}50\\ \times\ .10\end{array}}{ \ \ \ \space 5.00}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/912804/gif.latex)
![\frac{\begin{array}[b]{r}50.00\\ -\ 5.00\end{array}}{ \ \ \space 45.00}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/912806/gif.latex)






![\frac{\begin{array}[b]{r}40\\ \times\ .20\end{array}}{ \ \ \ \space 8.00}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/912733/gif.latex)
![\frac{\begin{array}[b]{r}40.00\\ -\ 8.00\end{array}}{ \ \ \space 32.00}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/912735/gif.latex)






![\frac{\begin{array}[b]{r}57\\ \times\ .20\end{array}}{ \ \ \ \space 11.40}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/912828/gif.latex)
![\frac{\begin{array}[b]{r}57.00\\ -\ 11.40\end{array}}{ \ \ \space 45.60}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/912830/gif.latex)






![\frac{\begin{array}[b]{r}31\\ \times\ .20\end{array}}{ \ \ \ \space 6.20}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/912781/gif.latex)
![\frac{\begin{array}[b]{r}31.00\\ -\ 6.20\end{array}}{ \ \ \space 24.80}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/912783/gif.latex)






![\frac{\begin{array}[b]{r}15\\ \times\ .20\end{array}}{ \ \ \ \space 3.00}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/912855/gif.latex)
![\frac{\begin{array}[b]{r}15.00\\ -\ 3.00\end{array}}{ \ \ \space 12.00}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/912857/gif.latex)


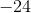












![\frac{\begin{array}[b]{r}11+x=0\\ -11\ \ \ \ -11\end{array}}{\\\\x=-11}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/913177/gif.latex)



