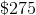Divide the number of revolutions by the number of minutes to get revolutions per minute:

$\displaystyle 330\div 15 = 22$,

making $\displaystyle 22$ revolutions per minute the correct choice.

First, find out how long it takes the factory to produce $\displaystyle 1$ tent.

$\displaystyle \frac{15}{300}=0.05$

Since it takes the factory $\displaystyle 0.05$ minutes to make $\displaystyle 1$ tent, multiply this number by $\displaystyle 9000$ to find how long it takes to make $\displaystyle 9000$ tents.

$\displaystyle 0.05\times9000=450$

It will take the factory $\displaystyle 450$ minutes to make $\displaystyle 9000$ tents.

First, find how many cans of soda Billy can drink in 1 day.

$\displaystyle \frac{12}{4}=3$

Since, he can drink $\displaystyle 3$ cans in $\displaystyle 1$ day, then the following equation will tell us how many cans he drinks in $\displaystyle 2$ days.

$\displaystyle 3\times2=6$

First, find the cost per marker.

$\displaystyle 45\div15=3$

Now, multiply this cost per marker by $\displaystyle 25$, the number of markers we want.

$\displaystyle 25\times3=75$

Set up the following proportion:

$\displaystyle \frac{2}{0.5}=\frac{200}{x}$,

where $\displaystyle x$ is the number of hours it'll take to empty $\displaystyle 200$ gallons.

Now solve for $\displaystyle x$.

$\displaystyle 2x=100$

$\displaystyle x=50$

First, figure out how long it takes Julie to read 1 page.

$\displaystyle 2\div5=0.4$

It takes Julie $\displaystyle 0.4$ minutes to read one page. Now, multiply this by the number of pages she needs to read to find out how long it will take her.

$\displaystyle 0.4\times120=48$

It will take Julie $\displaystyle 48$ minutes to read $\displaystyle 120$ pages.

Divide the time it take Dennis to paint $\displaystyle 8$ walls by the number of walls he painted to find how long it will take him to paint one wall.

$\displaystyle 120\div8=15$

It will take Dennis $\displaystyle 15$ minutes to paint one wall.

First, find out how much money it costs to play for one minute.

$\displaystyle 1.25\div3=0.41667$

Now, multiply this amount by the number of minutes in an hour to find how much it will cost for the player to play for one hour.

$\displaystyle 0.41667\times60=25$

It will cost her $\displaystyle \$25$ to play for one hour.

First, convert the minutes to hours.

$\displaystyle 45\div60=0.75$

Since $\displaystyle 45$ minutes is $\displaystyle 0.75$ hours, multiply this by the doctor's hourly rate to find how much it will cost to hire this doctor for $\displaystyle 45$ minutes.

$\displaystyle 500\times0.75=375$

Use the dentist's rate to find how much the first three hours of the appointment will cost.

$\displaystyle 50\times 3=150$

Next, use the dentist's second rate to find out how much the last five hours of the appointment will cost.

$\displaystyle 25\times5=125$

Now, add these values together to get the cost of the entire appointment.

$\displaystyle 150+125=275$