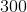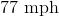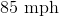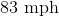All Common Core: 6th Grade Math Resources
Example Questions
Example Question #11 : Grade 6
Candidate A receives 


In order to solve this problem we need to create a ratio with the given information. It says that for every 

Now substitute in the given numbers.
We know that candidate B received 
Now, use the original relationship to create a proportion and solve for the number of votes that candidate A received.
Cross multiply and solve for 
Simplify and solve.
Example Question #12 : Grade 6
Candidate A receives 


In order to solve this problem we need to create a ratio with the given information. It says that for every 

Now substitute in the given numbers.
We know that candidate B received 
Now, use the original relationship to create a proportion and solve for the number of votes that candidate A received.
Cross multiply and solve for 
Simplify and solve.
Example Question #31 : Ratio And Proportion
A motorcycle travels 

In order to find the motorcyclist’s speed, we need to create a ratio of the miles travelled in a single hour.
Reduce and solve.
Example Question #38 : How To Find A Ratio
A motorcycle travels 

In order to find the motorcyclist’s speed, we need to create a ratio of the miles travelled in a single hour.
Reduce and solve.
Example Question #1 : Understand The Concept Of A Unit Rate: Ccss.Math.Content.6.Rp.A.2
A motorcycle travels 

In order to find the motorcyclist’s speed, we need to create a ratio of the miles travelled in a single hour.
Reduce and solve.
Example Question #2 : Understand The Concept Of A Unit Rate: Ccss.Math.Content.6.Rp.A.2
A motorcycle travels 

In order to find the motorcyclist’s speed, we need to create a ratio of the miles travelled in a single hour.
Reduce and solve.
Example Question #1 : Understand The Concept Of A Unit Rate: Ccss.Math.Content.6.Rp.A.2
A motorcyclist travels 

In order to find the motorcyclist’s speed, we need to create a ratio of the miles travelled in a single hour.
Reduce and solve.
Example Question #2 : Understand The Concept Of A Unit Rate: Ccss.Math.Content.6.Rp.A.2
A motorcycle travels 

In order to find the motorcyclist’s speed, we need to create a ratio of the miles travelled in a single hour.
Reduce and solve.
Example Question #5 : Understand The Concept Of A Unit Rate: Ccss.Math.Content.6.Rp.A.2
A motorcycle travels 

In order to find the motorcyclist’s speed, we need to create a ratio of the miles travelled in a single hour.
Reduce and solve.
Example Question #6 : Understand The Concept Of A Unit Rate: Ccss.Math.Content.6.Rp.A.2
A motorcycle travels 

In order to find the motorcyclist’s speed, we need to create a ratio of the miles travelled in a single hour.
Reduce and solve.
Certified Tutor
Certified Tutor
All Common Core: 6th Grade Math Resources