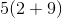All Common Core: 6th Grade Math Resources
Example Questions
Example Question #471 : The Number System
Use the distributive property to express the sum 
None of these
The distributive property can be used to rewrite an expression. When we use this property we will identify and pull out the greatest common factor of each of the addends. Then we can create a quantity that represents the sum of two whole numbers with no common factor multiplied by their greatest common factor.
In this case, the greatest common factor shared by each number is:
After we reduce each addend by the greatest common factor we can rewrite the expression:
Example Question #471 : The Number System
Use the distributive property to express the sum 
The distributive property can be used to rewrite an expression. When we use this property we will identify and pull out the greatest common factor of each of the addends. Then we can create a quantity that represents the sum of two whole numbers with no common factor multiplied by their greatest common factor.
In this case, the greatest common factor shared by each number is:
After we reduce each addend by the greatest common factor we can rewrite the expression:
Example Question #1613 : Grade 6
Use the distributive property to express the sum 
None of these
The distributive property can be used to rewrite an expression. When we use this property we will identify and pull out the greatest common factor of each of the addends. Then we can create a quantity that represents the sum of two whole numbers with no common factor multiplied by their greatest common factor.
In this case, the greatest common factor shared by each number is:
After we reduce each addend by the greatest common factor we can rewrite the expression:
Example Question #1 : Find Greatest Common Factor And Least Common Multiple: Ccss.Math.Content.6.Ns.B.4
Use the distributive property to express the sum 
The distributive property can be used to rewrite an expression. When we use this property we will identify and pull out the greatest common factor of each of the addends. Then we can create a quantity that represents the sum of two whole numbers with no common factor multiplied by their greatest common factor.
In this case, the greatest common factor shared by each number is:
After we reduce each addend by the greatest common factor we can rewrite the expression:
Example Question #1 : Find Greatest Common Factor And Least Common Multiple: Ccss.Math.Content.6.Ns.B.4
Use the distributive property to express the sum 
None of these
The distributive property can be used to rewrite an expression. When we use this property we will identify and pull out the greatest common factor of each of the addends. Then we can create a quantity that represents the sum of two whole numbers with no common factor multiplied by their greatest common factor.
In this case, the greatest common factor shared by each number is:
After we reduce each addend by the greatest common factor we can rewrite the expression:
Example Question #1401 : Numbers And Operations
Use the distributive property to express the sum 
The distributive property can be used to rewrite an expression. When we use this property we will identify and pull out the greatest common factor of each of the addends. Then we can create a quantity that represents the sum of two whole numbers with no common factor multiplied by their greatest common factor.
In this case, the greatest common factor shared by each number is:
After we reduce each addend by the greatest common factor we can rewrite the expression:
Example Question #3 : Find Greatest Common Factor
Use the distributive property to express the sum 
None of these
The distributive property can be used to rewrite an expression. When we use this property we will identify and pull out the greatest common factor of each of the addends. Then we can create a quantity that represents the sum of two whole numbers with no common factor multiplied by their greatest common factor.
In this case, the greatest common factor shared by each number is:
After we reduce each addend by the greatest common factor we can rewrite the expression:
Example Question #6 : Find Greatest Common Factor
Use the distributive property to express the sum 
The distributive property can be used to rewrite an expression. When we use this property we will identify and pull out the greatest common factor of each of the addends. Then we can create a quantity that represents the sum of two whole numbers with no common factor multiplied by their greatest common factor.
In this case, the greatest common factor shared by each number is:
After we reduce each addend by the greatest common factor we can rewrite the expression:
Example Question #2 : Find Greatest Common Factor And Least Common Multiple: Ccss.Math.Content.6.Ns.B.4
Use the distributive property to express the sum 
None of these
The distributive property can be used to rewrite an expression. When we use this property we will identify and pull out the greatest common factor of each of the addends. Then we can create a quantity that represents the sum of two whole numbers with no common factor multiplied by their greatest common factor.
In this case, the greatest common factor shared by each number is:
After we reduce each addend by the greatest common factor we can rewrite the expression:
Example Question #2 : Find Greatest Common Factor And Least Common Multiple: Ccss.Math.Content.6.Ns.B.4
Use the distributive property to express the sum 
The distributive property can be used to rewrite an expression. When we use this property we will identify and pull out the greatest common factor of each of the addends. Then we can create a quantity that represents the sum of two whole numbers with no common factor multiplied by their greatest common factor.
In this case, the greatest common factor shared by each number is:
After we reduce each addend by the greatest common factor we can rewrite the expression:
Certified Tutor
Certified Tutor
All Common Core: 6th Grade Math Resources