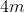All Common Core: 4th Grade Math Resources
Example Questions
Example Question #90 : How To Find The Area Of A Rectangle
What is the length of a rectangular yard with an area of 
We have the area and the width, so we can plug those values into our equation and solve for our unknown.
Example Question #53 : Solving For Length
What is the length of a rectangular yard with an area of 
We have the area and the width, so we can plug those values into our equation and solve for our unknown.
Example Question #231 : Geometry
What is the length of a rectangular yard with an area of 
We have the area and the width, so we can plug those values into our equation and solve for our unknown.
Example Question #91 : How To Find The Area Of A Rectangle
What is the length of a rectangular yard with an area of 
We have the area and the width, so we can plug those values into our equation and solve for our unknown.
Example Question #92 : How To Find The Area Of A Rectangle
What is the length of a rectangular yard with an area of 
We have the area and the width, so we can plug those values into our equation and solve for our unknown.
Example Question #141 : Solve Problems Involving Measurement And Conversion Of Measurements
What is the length of a rectangular yard with an area of 
We have the area and the width, so we can plug those values into our equation and solve for our unknown.
Example Question #64 : Apply Area And Perimeter Formulas For Rectangles: Ccss.Math.Content.4.Md.A.3
What is the length of a rectangular yard with an area of 
We have the area and the width, so we can plug those values into our equation and solve for our unknown.
Example Question #241 : Quadrilaterals
What is the length of a rectangular yard with an area of 
We have the area and the width, so we can plug those values into our equation and solve for our unknown.
Example Question #66 : Apply Area And Perimeter Formulas For Rectangles: Ccss.Math.Content.4.Md.A.3
What is the length of a rectangular yard with an area of 
We have the area and the width, so we can plug those values into our equation and solve for our unknown.
Example Question #67 : Apply Area And Perimeter Formulas For Rectangles: Ccss.Math.Content.4.Md.A.3
What is the length of a rectangular yard with an area of 
We have the area and the width, so we can plug those values into our equation and solve for our unknown.
Certified Tutor
Certified Tutor
All Common Core: 4th Grade Math Resources