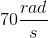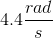All College Physics Resources
Example Questions
Example Question #1 : Motion
A rock is tossed horizontally off the edge of a cliff with a velocity of 

This question requires an understanding of motion in two dimensions. The most important concept in this question is that the motion in each dimension is independent. Since the rock's initial velocity is purely in the horizontal direction, the initial velocity has no impact on the vertical velocity at any point. Likewise, the vertical acceleration has no impact on the horizontal speed. The rock will travel at 
To solve this problem, the first step is to set up an expression for the horizontal and vertical velocities as a function of time:
Thus,
Substituting 



Example Question #2 : Motion
A projectile reaches it max height in 

We first must find the initial vertical velocity (
We know that 
we also know that 
So plugging in what we know:
Knowing that 

Example Question #3 : Motion
If an object strikes the ground at 
First let's make a table of what we know:

It should also be noted it is simpler to define things so that the initial height is zero, so we don't have to deal with a bunch of negative numbers.
Also, since it is dropped vertically and we are only interested in the height it is dropped from we aren't interested in any information regarding the projectile's horizontal motion.
Let's use the equation:
since
We can solve for 
This is our final answer.
Example Question #4 : Motion
A projectile is launched vertically upwards at 
First let's write down the information we're given:


Let's use the equation
to solve for the time it takes the projectile to reach its max height.
Solving for 
Now lets plug in what we know and calculate the time:

Example Question #12 : Mechanics
A projectile is launched vertically upwards at 
First let's write down the information we're given:


Let's use the following equation to solve for the time it takes the projectile to reach its max height:
Solving for 
Now lets plug in what we know and calculate the time:
Since the projectile takes twice as long to land as its does to reach its max height we simply multiple the 


Example Question #6 : Motion
If a particle reaches its max height in 



First let's write out the information we are given:
We know that in order to obtain the time it takes a projectile to hit the ground we just multiply 

Now we can use the equation
Since we are only concerned with the particle's motion in the horizontal direction, and we know that the horizontal velocity is constant 

This gives us:
Let's plug in what we have:



Example Question #1 : Motion In Two Dimensions
A cannon is being shot from the ground. You want to shoot that cannon as far as possible. At what angle should the cannon be shot?
60 degrees
30 degrees
45 degrees
90 degrees
50 degrees
45 degrees
There are many explanations for this. First you could simply insert a velocity at all of these angles and see which ends up with the greatest change in horizontal distance. You also could use basic calculus and solve for the greatest theta.
Example Question #31 : College Physics
A ball is thrown off a building at a speed of 


This is a projectile motion problem. The problem states that it was thrown off the building at an angle of 30 degrees to the horizontal. So before we can find time, we need to find the horizontal and vertical parts of this velocity.
Since 
It follows that

Now, before we can find far it went, we need to find how long it was in the air. We need to solve for time.
With the equation 
X is the initial height which in this case is the 

Plugging all that in and solving yields
Knowing that the time the ball is in the air is 

Example Question #1 : Harmonic Motion
A pendulum is made up of a small 


The angular frequency of a simple pendulum is 

Example Question #1 : Harmonic Motion
Which of the following is not an example of simple harmonic motion?
A book falling to the ground
A child swinging on a swing set
The mass on a pendulum moving back and forth
A plucked string vibrating on a guitar
A book falling to the ground
For this question, we need to recall what simple harmonic motion is. Remember that it is a periodic motion where the restoring force depends on the displacement of the object undergoing these motions. So to answer this question, we need to keep this idea in mind and see which example doesn't match up.
A mass on a pendulum moving back and forth is clearly an example of simple harmonic motion. As the mass moves further from the center in either direction, it experiences a greater and greater force in the opposite direction.
A child swinging on a swing set is another correct example. This situation is analogous to the mass on a pendulum swinging back and forth.
A vibrating guitar string is yet another example of simple harmonic motion. After it is plucked, the string oscillates back and forth.
Finally, a book falling to the ground does not represent harmonic motion. Once the book is released from rest, we intuitively know that it will fall to the ground and will then stay there; in no way is there any periodic motion.
Certified Tutor
All College Physics Resources









![speed_{total}=\sqrt{(5\frac{m}{s})^2+[(0.5)(9.81\frac{m}{s^2})t^2]^2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/956612/gif.latex)









































![\frac{(0-17)}{[-10]}=t=1.7s](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1002383/gif.latex)