All College Algebra Resources
Example Questions
Example Question #1 : Solving Logarithms
Solve for 
To solve for 
Now, with the same base, the exponents can be set equal to each other:
Solving for 
Example Question #1 : Solving Logarithms
Solve the equation:
Example Question #3 : Solving Logarithms
Solve for 
Rewrite in exponential form:
Solve for x:
Example Question #1 : Solving And Graphing Logarithms
Solve the following equation:
For this problem it is helpful to remember that,


Therefore we can set what is inside of the parentheses equal to each other and solve for 
Example Question #1 : Solving Logarithmic Functions
Solve this logarithmic equation:
None of the other answers.
To solve this problem you must be familiar with the one-to-one logarithmic property.

one-to-one property:
isolate x's to one side:
move constant:
Example Question #1 : Solving Logarithmic Functions
Solve the equation:
No solution exists
Get all the terms with e on one side of the equation and constants on the other.
Apply the logarithmic function to both sides of the equation.
Example Question #51 : College Algebra
Solve the equation:
Recall the rules of logs to solve this problem.
First, when there is a coefficient in front of log, this is the same as log with the inside term raised to the outside coefficient.
Also, when logs of the same base are added together, that is the same as the two inside terms multiplied together.
In mathematical terms:
Thus our equation becomes,
To simplify further use the rule,

Example Question #54 : Exponential And Logarithmic Functions
Solve the following equation for t
Solve the following equation for t
We can solve this equation by rewriting it as an exponential equation:
Next, take the fourth root to get:
We can check our work vie the following:
Example Question #5 : Solving Logarithmic Functions
Solve for 
It is impossible to isolate 
The first step step is to carry out the inverse operation of the natural logarithm,
We can use the property 
Solve for 
Example Question #4 : Solving Logarithmic Functions
Solve this equation:
None of these.
No solution.
Note that this equation is a quadratic because
Factor:
Set each factor equal to 0 and solve:
All College Algebra Resources





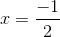













































































![t=\sqrt[4]{625}=5](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/699591/gif.latex)


























