All College Algebra Resources
Example Questions
Example Question #2 : College Algebra
Solve the following for x:
To solve, you must first "undo" the log. Since no base is specified, you assume it is 10. Thus, we need to take 10 to both sides.
Now, simply solve for x.
Example Question #2 : Logarithmic Functions
Simplify the following:
To solve, you must combine the logs into 1 log, instead of three separate ones. To do this, you must remember that when adding logs, you multiply their insides, and when you subtract them, you add their insides. Therefore,
Example Question #3 : Logarithmic Functions
Solve for y in the following expression:
To solve for y we first need to get rid of the logs.
Then we get .
After that, we simply have to divide by 5x on both sides:
Example Question #4 : Logarithmic Functions
Solve for .
To solve this natural logarithm equation, we must eliminate the operation. To do that, we must remember that is simply with base . So, we raise both side of the equation to the power.
This simplifies to
. Remember that anything raised to the 0 power is 1.
Continuing to solve for x,
Example Question #5 : Logarithmic Functions
Solve for .
To eliminate the operation, simply raise both side of the equation to the power because the base of the operation is 7.
This simplifies to
Example Question #6 : Logarithmic Functions
;
True or false:
if and only if either or .
False
True
False
is a direct statement of the Change of Base Property of Logarithms. If and , this property holds true for any - not just .
Example Question #7 : Logarithmic Functions
Evaluate
is an undefined quantity.
is an undefined quantity.
is undefined for two reasons: first, the base of a logarithm cannot be negative, and second, a negative number cannot have a logarithm.
Example Question #7 : Logarithmic Functions
Use the properties of logarithms to rewrite as a single logarithmic expression:
, so
, so the above becomes
, so the above becomes
Example Question #8 : Logarithmic Functions
Use the properties of logarithms to rewrite as a single logarithmic expression:
None of the other choices gives the correct response.
, so
, so the above becomes
By the Change of Base Property,
, so the above becomes
,
the correct response.
Example Question #9 : Logarithmic Functions
Expand the logarithm:
None of these
We expand this logarithm based on the property:
and .
Certified Tutor
All College Algebra Resources





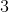































































































![\ln \sqrt[3]{\frac{x}{y}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1036013/gif.latex)






![\ln \sqrt[3]{\frac{x}{y}}\rightarrow\frac{1}{3}\ln\frac{x}{y}\rightarrow \boldsymbol{\frac{1}{3}(\ln x-\ln y)}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1036016/gif.latex)



