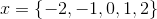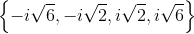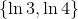We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

College Algebra : Equations Reducible to Quadratic Form

Study concepts, example questions & explanations for College Algebra

Create An Account

All College Algebra Resources

5 Diagnostic Tests 84 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #41 : Solving Equations And Inequallities

Solve x^4-7x^2+12=0

Possible Answers:

$x=-\sqrt{3}$

x=-2

$x=\pm\sqrt{3}$

$x=\pm2$

$x=\sqrt{3}$

x=2

There are no solutions

Correct answer:

$x=\pm\sqrt{3}$

$x=\pm2$

Explanation:

To make this problem easier, lets start off by doing a u-substitution.

Let u=x^2 .

x^4-7x^2+12=0

u^2-7u+12=0

Now we can factor the left hand side.

(u-3)(u-4)=0

We have two solutions for , now we can plug those into u=x^2 , to get all the solutions.

$x^2=3\rightarrow x=\pm\sqrt{3}$

$x^2=4\rightarrow x=\pm\sqrt{4}=\pm2$

Report an Error

Example Question #2 : Equations Reducible To Quadratic Form

Find all real roots of the polynomial function

f(x)=x^5-2x^3+x

Possible Answers:

$x = \left \{ -2,-1,0,1,2\right \}$

$x = \left \{ -1,1\right \}$

$x = \left \{ -1,0,1\right \}$

x=0 (There are no nonzero solutions)

$x = \left \{ 0,1\right \}$

Correct answer:

$x = \left \{ -1,0,1\right \}$

Explanation:

Find the roots of the polynomial,

f(x)=x^5-2x^3+x

Set f(x) equal to

x^5 -2x^3-x = 0

Factor out ,

x(x^4-2x^2-1)=0

Notice that the the factor x^4-2x^2-1 is a quadratic even though it might not seem so at first glance. One way to think of this is as follows:

Let u = x^2

Then we have u^2 = x^4 , substitute into x^4-2x^2-1 to get,

u^2-2u+1 = 0

Notice that the change in variable from to u=x^2 has resulted in a quadratic equation that can be easily factored due to the fact that it is a square of a simple binomial:

(u-1)^2=0

The solution for is,

u = 1

Because u = x^2 we go back to the variable ,

x^2 = 1

Therefore, the roots of the x^4-2x^2+1 factor are,

$x = \pm 1$

The other root of f(x) is x = 0 since the function clearly equals when x=0 .

The solution set is therefore, $x = \left \{ -1,0,1\right \}$

Below is a plot of f(x)=x^5 - 4x^3 +x . You can see where the function intersects the -axis at points corresponding to our solutions.

Further Discussion

The change of variable was a tool we used to write the quadratic factor in a more familiar form, but we could have just factored the original function in terms of as follows,

x(x^4-2x^2+1)

=x(x^2-1)^2

=x(x^2-1)(x^2-1)

=x(x-1)(x+1)(x-1)(x+1)

Setting this to zero gives the same solution set, $x = \left \{ -1,0,1\right \}$

Report an Error

Example Question #3 : Equations Reducible To Quadratic Form

Give the complete solution set for the equation:

$x^{4} + 8x^{2} + 12 = 0$

Possible Answers:

$\left \{ - \sqrt{6}, - \sqrt{2}, \sqrt{2} , \sqrt{6} \right \}$

$\left \{ - 2, - \sqrt{3}, \sqrt{3} ,2 \right \}$

$\left \{ - i \sqrt{6}, - i \sqrt{2}, i \sqrt{2} , i \sqrt{6} \right \}$

$\left \{ -2 i \sqrt{3}, - i , i ,2 i \sqrt{3}\right \}$

$\left \{ -2 i , - i \sqrt{3}, i \sqrt{3} ,2 i \right \}$

Correct answer:

$\left \{ - i \sqrt{6}, - i \sqrt{2}, i \sqrt{2} , i \sqrt{6} \right \}$

Explanation:

$x^{4} + 8x^{2} + 12 = 0$

can be rewritten in quadratic form by setting $u = x^{2}$ , and, consequently, $u^{2} = x^{4}$ ; the resulting equation is as follows:

$u^{2} + 8u+ 12 = 0$

By the reverse-FOIL method we can factor the trinomial at left. We are looking for two integers with sum 8 and product 12; they are 2 and 6, so the equation becomes

(u+ 6)(u+ 2) = 0

Setting both binomials equal to 0, it follows that

u = -2 or u = -6 .

Substituting $x^{2}$ for , we get

$x^{2} = -2$ ,

in which case

$x = \pm i \sqrt{2}$ ,

or $x^{2} = -2$

in which case

$x = \pm i \sqrt{6}$ .

The solution set is $\left \{ - i \sqrt{6}, - i \sqrt{2}, i \sqrt{2} , i \sqrt{6} \right \}$ .

Report an Error

Example Question #1 : Equations Reducible To Quadratic Form

Give the complete set of real solutions for the equation:

$e^{2x}- 8e^{x}+ 12 = 0$

Possible Answers:

$\left \{ \ln 2, \ln 6 \right \}$

$\left \{ 0, \ln 12 \right \}$

The equation has no solutions.

$\left \{ \ln 3 , \ln 4 \right \}$

Correct answer:

$\left \{ \ln 2, \ln 6 \right \}$

Explanation:

$e^{2x}- 8e^{x}+ 12 = 0$

can be rewritten in quadratic form by setting $u = e^{x}$ , and, consequently, $u^{2} =( e^{x})^{2} = e^{2x}$ ; the resulting equation is as follows:

$u^{2} - 8u+ 12 = 0$

By the reverse-FOIL method we can factor the trinomial at left. We are looking for two integers with sum 8 and product 12; they are and , so the equation becomes

(u-6)(u- 2) = 0

Setting both binomials equal to 0, it follows that

u =2 or u = 6 .

Substituting $e^{x}$ for , we get

$e^{x} = 2$

in which case

$x = \ln 2$ ,

and

$e^{x} = 6$ ,

in which case

$x = \ln 6$

The set of real solutions is therefore $\left \{ \ln 2, \ln 6 \right \}$ .

Report an Error

View College Algebra Tutors

Zara
Certified Tutor

University of Manitoba, Bachelor in Arts, Mathematics.

View College Algebra Tutors

George
Certified Tutor

Pensacola State College, Bachelor in Arts, Mathematics.

View College Algebra Tutors

Shakeel
Certified Tutor

All College Algebra Resources

5 Diagnostic Tests 84 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Algebra Tutors in Washington DC, French Tutors in New York City, Chemistry Tutors in Atlanta, ACT Tutors in Houston, Calculus Tutors in Miami, Biology Tutors in Houston, ISEE Tutors in Dallas Fort Worth, Calculus Tutors in Atlanta, SAT Tutors in Washington DC, MCAT Tutors in Washington DC

Popular Courses & Classes

SSAT Courses & Classes in San Diego, Spanish Courses & Classes in New York City, SAT Courses & Classes in Dallas Fort Worth, GRE Courses & Classes in Chicago, LSAT Courses & Classes in Miami, SSAT Courses & Classes in Dallas Fort Worth, GMAT Courses & Classes in San Francisco-Bay Area, Spanish Courses & Classes in Dallas Fort Worth, LSAT Courses & Classes in Denver, SAT Courses & Classes in Los Angeles

Popular Test Prep

ACT Test Prep in Los Angeles, SAT Test Prep in Seattle, ISEE Test Prep in New York City, SSAT Test Prep in Seattle, MCAT Test Prep in Boston, ACT Test Prep in Washington DC, GMAT Test Prep in Los Angeles, MCAT Test Prep in Washington DC, ACT Test Prep in New York City, MCAT Test Prep in Philadelphia

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

College Algebra : Equations Reducible to Quadratic Form

Study concepts, example questions & explanations for College Algebra

All College Algebra Resources

Example Questions

Example Question #41 : Solving Equations And Inequallities

Example Question #2 : Equations Reducible To Quadratic Form

Example Question #3 : Equations Reducible To Quadratic Form

Example Question #1 : Equations Reducible To Quadratic Form

All College Algebra Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: