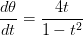If this function gives the position, the first derivative will give its speed. To differentiate, use the chain rule: . In this case,  and . Since  and , the first derivative is . 

Plug in  for t: 

To find when the particle changes direction, we need to find the critical values of . This is done by finding the velocity function, setting it equal to , and solving for 

.

Hence .

The solutions to this on the unit circle are , so these are the values of  where the particle would normally change direction. However, our given interval is , which does not contain . Hence the particle does not change direction on the given interval.

To find the acceleration of the particle, we must take the first derivative of the velocity function:

The derivative was found using the following rule:

Now, we evaluate the acceleration function at the given point:

Acceleration is the rate of change of velocity, so we must integrate the acceleration function to find the velocity function:

The integration was performed using the following rules:

, 

To find the integration constant C, we must use the initial condition given:

Our final answer is

The velocity of a particle is given by v(t). Find the function which models the particle's acceleration.

To find the acceleration from a velocity function, simply take the derivative.

In this case, we are given v(t), and we need to find v'(t) because v'(t)=a(t).

To find v'(t), we need to use the power rule. 

For each term, simply multiply by the exponent, and then subtract one from the exponent. Constant terms will drop out, linear terms will become constants, and so on.

So, our answer is:

The velocity of a particle is given by . Find the particle's acceleration when .

To find the acceleration from a velocity function, simply take the derivative.

In this case, we are given , and we need to find  because .

To find , we need to use the power rule. 

For each term, simply multiply by the exponent, and then subtract one from the exponent. Constant terms will drop out, linear terms will become constants, and so on.

So, our acceleration function is:

Now, plug in  for  and solve.

So, our answer is .

A right triangle has sides of lenght  and  which are both increasing in length over time such that: 

Find the rate at which the angle  opposite  is changing with respect to time.

a) First, we need to write an expression for the angle  as a function of . Because the angle is opposite the side  we know that the tangent is simply . Take the inverse of the tangent: 

Now we need to differentiate with respect to . 

Recall the general derivative for the inverse tangent function is:

Applying this to our function for , and remembering to use the chain rule, we obtain: 

To determine the rate of change of the surface area of the spherical bubble, we must relate it to something we do know the rate of change of - the volume. 

The volume of a sphere is given by the following:

The rate of change of the volume is given by the derivative with respect to time:

The derivative was found using the following rules:

, 

We must now solve for the rate of change of the radius at the specified radius, so that we can later solve for the rate of change of surface area:

Next, we must find the surface area and rate of change of the surface area of the sphere the same way as above:

Plugging in the known rate of change of the surface area at the specified radius, and this radius into the rate of surface area change function, we get

To find the rate of change of the diameter, we must relate the diameter to something we do know the rate of change of: the surface area.

The surface area of the top side of the pizza dough is given by

The rate of change, then, is found by taking the derivative of the function with respect to time:

Solving for the rate of change of the radius at the given radius, we get

 inches/sec

Now, we relate the diameter to the radius of the pizza dough:

Taking the derivative of both sides with respect to time, we get

Plugging in the known rate of change of the radius at the given radius, we get

 inches/sec

We could have found this directly by writing our surface area formula in terms of diameter, however the process we used is more applicable to problems in which the related rate of change is of something not as easy to manipulate.

To determine the rate of change of the circumference at a given radius, we must relate the circumference rate of change to the rate of change we know - that of the volume.

Starting with the equation for the volume of the spherical balloon,

we take the derivative of the function with respect to time, giving us the rate of change of the volume:

The derivative was found using the following rules:

, 

The chain rule was used when taking the derivative of the radius with respect to time, because we know that it is a function of time.

Solving for  using our known  at the given radius, we get

Now, we use this rate of change and apply it to the rate of change of the circumference, which we get by taking the derivative of the circumference with respect to time:

Solving for the rate of change of the circumference by plugging in the known rate of change of the radius, we get