All Calculus 2 Resources
Example Questions
Example Question #31 : L'hospital's Rule
If you plug in the limit value, the function turns into 


Example Question #31 : L'hospital's Rule
Evaluate: 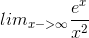
Limit Does Not Exist
Example Question #33 : L'hospital's Rule
Find the limit using L'Hospital's Rule.
We rewrite the limit as
Substituting 
L'Hospital's Rule states that when the limit is in indeterminate form, the limit becomes
For 

and substituting 
As such
Example Question #34 : L'hospital's Rule
Find the limit using L'Hospital's Rule.
Substituting 
L'Hospital's Rule states that when the limit is in indeterminate form, the limit becomes
For 

and substituting 
As such
Example Question #35 : L'hospital's Rule
Evaluate the following limit:
Simply substituting 

Because direct substitution yields an indeterminate result, we must apply L'Hospital's rule to the limit:
if and only if 



Here,


Hence,
Example Question #36 : L'hospital's Rule
Evaluate the following limit:
When evaluating the limit using normal methods (substitution), we receive the indeterminate form 
Using the formula above for our limit, we get
The derivatives were found using the following rules:


Example Question #37 : L'hospital's Rule
Evaluate the limit:
When evaluating the limit using normal methods (substitution), we get the indeterminate form 
Using the above formula for our limit, we get
The derivatives were found using the following rule:
Example Question #38 : L'hospital's Rule
Evaluate the following limit, if possible:
The limit does not exist.
To calculate the limit we first plug the limit value into the numerator and denominator of the expression. When we do this we get 



then

We are evaluating the limit

In this case we have

and

We differentiate both functions and find

and

By L'Hopital's rule

When we plug the limit value of 2 into this expression we get 9/3, which simplifies to 3.
Example Question #39 : L'hospital's Rule
Evaluate the following limit, if possible:

The limit does not exist.
If we plugged in the limit value, 




then

The limit we wish to evaluate is

so in this case
and

We calculate the derivatives of both of these functions and find that
and

Thus

When we plug the limit value, 


Example Question #40 : L'hospital's Rule
Evaluate the following limit, if possible:

The limit does not exist
The limit does not exist
We will show that the limit does not exist by showing that the limits from the left and right are different.
We will start with the limit from the right. Using the product rule we rewrite the limit

We know that
and
so

We calculate the limit from the left in the same way and find

Thus the two-sided limit does not exist.
All Calculus 2 Resources





















































































