All Calculus 2 Resources
Example Questions
Example Question #51 : Applications In Physics
If 

Recall that the integral of the velocity function is the position function:
Now, integrate:
Now plug in your initial conditions:
Plug your C back into your position function:
Example Question #52 : Applications In Physics
If 

Recall that the integral of velocity is the position function:
Now, integrate. Remember to raise the exponent by 1 and also put that result on the denominator:
Now plug in your initial conditions to solve for C:
Now plug your C back in to your position function:
Example Question #53 : Applications In Physics
If 

Recall that the integral of the velocity function is the position function:
Now, integrate. Remember to raise the exponent by 1 and also put that result on the denominator:
Now, plug in your initial conditions:
Now plug your C back into your position function:
Example Question #54 : Applications In Physics
In the vacuum of space, a particle is initially moving at a constant speed of only 6 meters/second away from you as you watch in your space capsule stationary relative to the particle. You track the object and then observe an acceleration that varies with time as,
After travelling for 20 minutes at this speed the particle is now 
To solve the problem we first need to find the position function by successively integrating. First find the velocity function by integrating the acceleration:
The constant of integration 
Now we integrate the velocity function to find the position function:
The constant of integration 







Now solve for
Example Question #221 : Integrals
Give the area of the region bounded by the curves of the functions
and

The two curves intersect when 
Therefore, the area between the curves is
Example Question #231 : Integrals
Give the area of the region bounded by the curves of the functions
and

The two curves intersect when


or
Therefore, the area between the curves is
Example Question #52 : Integral Applications
Give the area of the region bounded by the curves of the functions
and

The two curves intersect when

So the curves intersect at three points: 
The area of the region bound by the curves is
Example Question #1981 : Calculus Ii
Give the area of the region bounded by the curves of the functions

and

The two curves intersect when

or
Since it can be assumed that 
Therefore, either 



Therefore, the area between the curves is
Example Question #1 : Area Under A Curve
Find the area under the curve 


The area under a curve f(x) between two x-values 

In this case, 
![= [e^x]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/388784/gif.latex)

Example Question #2 : Area Under A Curve
Find the area between 



The first step to find the area between two curves is to set them equal to each other and find their intersection points.
The next step is to find which curve is "on the top" and which is "on the bottom" inside the interval 


Now, to find the area between the two curves, we take the integral from 

![\\\int_{0}^{1}(f(x) - g(x))dx\\ \int_{0}^{1}(\sqrt{x} - x^3)dx\\ \left [ \frac{2}{3}x^{3/2} - \frac{1}{4}x^4 \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/388801/gif.latex)

All Calculus 2 Resources

















































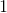






![\left |\int_{1}^{3} \left [g(x) - f(x) \right ] \mathrm{d}x \right |](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/180811/gif.latex)



















![\left |\int_{0}^{\ln 3} \left [g(x) - f(x) \right ] \mathrm{d}x \right |](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/181237/gif.latex)


































































