Call Now to Set Up Tutoring:

(888) 888-0446

Calculus 2 : Integral Applications

Study concepts, example questions & explanations for Calculus 2

Create An Account

All Calculus 2 Resources

9 Diagnostic Tests 308 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #301 : Integrals

Approximate the length of the curve of $f (x) = \ln (x + 1)$ on the interval [0,2] . Use Simpson's Parabolic Rule with n = 4 to make your estimate to the nearest thousandth.

Possible Answers:

2.486

2.303

2.198

2.442

2.667

Correct answer:

2.303

Explanation:

The length of the curve of f(x) on the interval [a,b] can be determined by evaluating the integral

$\int_{a}^{b} \sqrt{1 + f'(x) ^{2}} \; \mathrm{d}x$ .

$f (x) = \ln (x + 1)$ , so

$f'(x) = \frac{1}{x+1}$ , and the integral to be approximated is

$\int_{0}^{2} \sqrt{1 + \left ( \frac{1}{x+1} \right ) ^{2}} \; \mathrm{d}x$

$= \int_{0}^{2} \sqrt{\frac{x^{2}+2x+1}{x^{2}+2x+1} + \frac{1}{x^{2}+2x+1} } \; \mathrm{d}x$

$= \int_{0}^{2} \sqrt{\frac{x^{2}+2x+2}{x^{2}+2x+1} } \; \mathrm{d}x$

We divide the interval [0,2] into four subintervals of width $\Delta x = 2 \div 4 = 0.5$ each, so

$x_{0} = 0, x_{1} = 0.5, x_{2} = 1, x_{3} = 1.5, x_{4} = 2$

By Simpson's rule, we can estimate the integral by evaluating

$\frac{\Delta x}{3} \left ( g (x_{0}) + 4g(x_{1}) + 2g(x_{2}) + 4 g (x_{3}) + g (x_{4}) \right )$

$= \frac{0.5 }{3} \left ( g (0) + 4g(0.5) + 2g(1) + 4 g (1.5) + g (2) \right )$

where $g(x) = \sqrt{\frac{x^{2}+2x+2}{x^{2}+2x+1}$

We evaluate at these points, then substitute:

$g(0) = \sqrt{\frac{0^{2}+2 \cdot 0+2}{0^{2}+2 \cdot 0+1} } \approx 1.4142$

$g(0.5) = \sqrt{\frac{0.5^{2}+2 \cdot 0.5+2}{0.5^{2}+2 \cdot 0.5+1} } \approx 1.2019$

$g(1) = \sqrt{\frac{1^{2}+2 \cdot 1+2}{1^{2}+2 \cdot 1+1} } \approx 1.1180$

$g(1.5) = \sqrt{\frac{1.5^{2}+2 \cdot 1.5+2}{1.5^{2}+2 \cdot 1.5+1} } \approx 1.0770$

$g(2) = \sqrt{\frac{2^{2}+2 \cdot 2+2}{2^{2}+2 \cdot 2+1} } \approx 1.0541$

The approximation is therefore

$\approx \frac{0.5 }{3} \left ( 1.4142 +4 \cdot 1.2019 + 2\cdot 1.1180 +4 \cdot 1.0770 +1.0541 \right )$

$\approx \frac{0.5 }{3} \left ( 1.4142 +4.8076 + 2.2360 +4.3080 +1.0541 \right )$

$\approx \frac{0.5 }{3} \left (13.8199 \right ) \approx 2.303$

Report an Error

Example Question #1 : Length Of Curve, Distance Traveled, Accumulated Change, Motion Of Curve

Give the arclength of the graph of the function $f(x) = \frac{2}{3} x \sqrt{x}$ on the interval $\left [ 0,3 \right ]$ .

Possible Answers:

$\frac{11}{3}$

$\frac{14}{3}$

$\frac{16}{3}$

Correct answer:

$\frac{14}{3}$

Explanation:

The length of the curve of f(x) on the interval [a,b] can be determined by evaluating the integral

$\int_{a}^{b} \sqrt{1 + f'(x) ^{2}} \; \mathrm{d}x$ .

$f(x) = \frac{2}{3} x \sqrt{x} = \frac{2}{3} x^{\frac{3}{2}}$

$f(x) = \frac{2}{3} \cdot \frac{3}{2} x^{\frac{1}{2}} = \sqrt{x}$ .

The above integral becomes

$\int_{0}^{3} \sqrt{1 + (\sqrt{x}) ^{2}} \; \mathrm{d}x$

$\int_{0}^{3} \sqrt{x+1} \; \mathrm{d}x$

Substitute u = x + 1 . Then $\frac{\mathrm{d} u}{\mathrm{d} x} = 1$ , $\mathrm{d} u = \mathrm{d} x$ , and the integral becomes

$\int_{1}^{4} \sqrt{u} \; \mathrm{d}u = \int_{1}^{4} u^{\frac{1}{2}} \; \mathrm{d}u$

$= \left.\begin{matrix} \frac{u^{\frac{3}{2}}}{\frac{3}{2}} \\ \\ \end{matrix}\right| \begin{matrix} 4\\ \\ 1 \end{matrix}$

$= \left.\begin{matrix} \frac{2u \sqrt{u}}{3} \\ \\ \end{matrix}\right| \begin{matrix} 4\\ \\ 1 \end{matrix}$

$= \frac{2 \cdot 4 \sqrt{4}}{3} - \frac{2 \cdot 1 \sqrt{1}}{3}$

$= \frac{2 \cdot 4 \cdot 2 }{3} - \frac{2 \cdot 1 \cdot 1}{3} = \frac{16}{3} - \frac{2}{3} =\frac{14}{3}$

Report an Error

Example Question #1 : Length Of Curve, Distance Traveled, Accumulated Change, Motion Of Curve

Give the arclength of the graph of the function $f(x) = \frac{1}{2} \ln \left ( \cos 2 x \right )$ on the interval $\left [ 0, \frac{\pi}{8} \right ]$ .

Possible Answers:

$1 + \sqrt{2}$

$\ln \left ( 1 + \sqrt{2} \right )$

$\frac{1}{2} \ln \left ( 1 + \sqrt{2} \right )$

$1+\frac{1 }{2} \ln 2$

$\frac{1 }{2}+\frac{1 }{2} \sqrt{2}$

Correct answer:

$\frac{1}{2} \ln \left ( 1 + \sqrt{2} \right )$

Explanation:

The length of the curve of f(x) on the interval [a,b] can be determined by evaluating the integral

$\int_{a}^{b} \sqrt{1 + f'(x) ^{2}} \; \mathrm{d}x$ .

$f(x) = \frac{1}{2} \ln \left ( \cos 2 x \right )$ , so

$f'(x) = \frac{1}{2} \cdot \frac{\frac{\mathrm{d} }{\mathrm{d} x}\cos 2 x}{\cos 2 x} = \frac{1}{2} \cdot \frac{-2 \sin 2x}{\cos 2 x} = - \tan 2x$

The integral becomes

$\int_{0}^{ \frac{\pi}{8}} \sqrt{1 + \left ( - \tan 2x \right )^{2}} \; \mathrm{d}x$

$= \int_{0}^{ \frac{\pi}{8}} \sqrt{1 + \tan ^{2} 2x } \; \mathrm{d}x$

$= \int_{0}^{ \frac{\pi}{8}} \sqrt{\sec ^{2} 2x } \; \mathrm{d}x$

$= \int_{0}^{ \frac{\pi}{8}} \sec 2x \; \mathrm{d}x$

Use substitution - set u = 2x . Then $\frac{\mathrm{d} u}{\mathrm{d} x} = 2$ , and $\mathrm{d} x = \frac{1}{2}\mathrm{d} u$ . The bounds of integration become $2 \cdot 0 = 0$ and $2 \cdot \frac{\pi}{8} = \frac{\pi}{4}$ , and the integral becomes

$\frac{1}{2} \int_{0}^{ \frac{\pi}{4}} \sec u \; \mathrm{d}u$

$=\left.\begin{matrix}\frac{1}{2} \ln | \sec u + \tan u | \\ \\ \end{matrix}\right|\begin{matrix} \frac{\pi}{4}\\ \\ 0 \end{matrix}$

$=\frac{1}{2} \ln \left | \sec \frac{\pi}{4} + \tan \frac{\pi}{4} \right | - \frac{1}{2} \ln | \sec 0 + \tan 0 |$

$=\frac{1}{2} \ln \left | \sqrt{2} + 1 \right | -\frac{1}{2} \ln | 1 + 0 |$

$=\frac{1}{2} \ln \left ( 1 + \sqrt{2} \right ) -\frac{1}{2} \ln 1$

$=\frac{1}{2} \ln \left ( 1 + \sqrt{2} \right ) - 0$

$=\frac{1}{2} \ln \left (1 + \sqrt{2} \right )$

Report an Error

Example Question #131 : Integral Applications

Give the arclength of the graph of the function $f(x) = \frac{1}{3} \left ( \cosh 3 x \right )$ on the interval $\left [ 0, 2 \right ]$ .

Possible Answers:

$\frac{ e^{6} +1 }{6e^{3}}$

$\frac{ e^{12} + 1 }{6e^{6}}$

$\frac{ e^{6} - 1 }{6e^{3}}$

$2e^{6}$

$\frac{ e^{12} - 1 }{6e^{6}}$

Correct answer:

$\frac{ e^{12} - 1 }{6e^{6}}$

Explanation:

The length of the curve of f(x) on the interval [a,b] can be determined by evaluating the integral

$\int_{a}^{b} \sqrt{1 + f'(x) ^{2}} \; \mathrm{d}x$ .

$f(x) = \frac{1}{3} \left ( \cosh 3 x \right )$ , so

$f'(x) = \frac{1}{3} \cdot 3 \sinh 3 x = \sinh 3 x$

and the integral becomes

$\int_{0}^{2} \sqrt{1 + \sinh^{2} 3 x } \; \mathrm{d}x$

$= \int_{0}^{2} \sqrt{ \cosh^{2} 3 x } \; \mathrm{d}x$

$= \int_{0}^{2} \cosh 3 x \; \mathrm{d}x$

Use substitution - set u =3x . Then $\frac{\mathrm{d} u}{\mathrm{d} x} = 3$ , and $\mathrm{d} x = \frac{1}{3}\mathrm{d} u$ . The bounds of integration become 0 and 6; the integral becomes

$= \int_{0}^{6} \frac{1}{3} \cosh u \; \mathrm{d}u$

$=\frac{1}{3} \int_{0}^{6} \cosh u \; \mathrm{d}u$

$= \frac{1}{3} \cdot \left.\begin{matrix} \sinh u\\ \\ \end{matrix}\right|\left.\begin{matrix} 6\\ \\ 0 \end{matrix}\right$

$=\frac{1}{3}\left ( \sinh 6 - \sinh 0 \right ) = \frac{1}{3} \sinh 6 =\frac{1}{3 } \cdot \frac{ e^{6} - e^{-6}}{2} = \frac{ \left (e^{6} - e^{-6} \right )e^{6}}{6e^{6}} = \frac{ e^{12} - 1 }{6e^{6}}$

Report an Error

Example Question #133 : Integral Applications

What is the average value of the function $f(x) = \tan x$ on the interval $\left [\frac{ \pi }{6} , \frac{ \pi }{3}\right ]$ ?

Possible Answers:

$\frac{ \pi \ln 3}{6}$

$\frac{3 \ln 3}{\pi}$

$\frac{6 \ln 3}{\pi}$

$\frac{ \ln 3}{\pi}$

$\frac{ \pi \ln 3}{3}$

Correct answer:

$\frac{3 \ln 3}{\pi}$

Explanation:

The average value of the function $f(x) = \tan x$ on the interval $\left [\frac{ \pi }{6} , \frac{ \pi }{3}\right ]$ is equal to

$\frac{1}{ \frac{ \pi}{3}-( \frac{ \pi}{6})} \int_{ \frac{ \pi}{6}}^{ \frac{ \pi}{3}}\tan x \cdot \mathrm{d}x$

$= \frac{1}{ \frac{ \pi}{6}} \int_{ \frac{ \pi}{6}}^{ \frac{ \pi}{3}}\tan x \cdot \mathrm{d}x$

$= \frac{6}{ \pi} \int_{ \frac{ \pi}{6}}^{ \frac{ \pi}{3}}\tan x \cdot \mathrm{d}x$

$= \frac{6}{ \pi} \cdot \left.\begin{matrix} \ln\left | \sec x \right |\\ \\ \end{matrix} \right | \begin{matrix} \frac{\pi}{3}\\ \\ \frac{ \pi}{6} \end{matrix}$

$= \frac{6}{ \pi} \left ( \ln\left | \sec \frac{ \pi}{3} \right | - \ln\left | \sec \frac{ \pi}{6} \right | \right )$

$= \frac{6}{ \pi} \left ( \ln 2 - \ln \frac{2\sqrt{3}}{3} \right )$

$= \frac{6}{ \pi} \ln \left (2 \div \frac{2\sqrt{3}}{3} \right )$

$= \frac{6}{ \pi} \ln \sqrt{3}= \frac{6}{ \pi} \cdot \frac{1}{2} \cdot \ln 3 = \frac{3 \ln 3}{\pi}$

Report an Error

Example Question #131 : Integral Applications

What is the average value of the function $f(x) = \frac{1}{x + 4}$ on the interval $\left [ -2, 2\right ]$ ?

Possible Answers:

$4 \ln 3$

$\frac{1}{3} \ln 4$

$\frac{1}{4} \ln 3$

$3 \ln 4$

$\ln 3$

Correct answer:

$\frac{1}{4} \ln 3$

Explanation:

The average value of the function $f(x) = \frac{1}{x + 4}$ on the interval $\left [ -2, 2\right ]$ is equal to

$\frac{1}{2-(-2)} \int_{-2}^{2} \frac{\mathrm{d}x}{x + 4}$

$=\frac{1}{4} \int_{-2}^{2} \frac{\mathrm{d}x}{x + 4}$

Substitute u = x+ 4 . Then $\frac{\mathrm{d} u}{\mathrm{d} x} = 1$ , and $\mathrm{d} x = \mathrm{d} u$ ; the bounds of integration become 2 and 6, and the above expression becomes

$=\frac{1}{4} \int_{2}^{6} \frac{\mathrm{d}u}{u}$

$=\frac{1}{4} \cdot \left.\begin{matrix} \ln |u| \\ \\ \end{matrix}\right| \begin{matrix} 6\\ \\ 2 \end{matrix}$

$=\frac{1}{4} \cdot \left ( \ln 6 - \ln 2 \right )$

$=\frac{1}{4} \ln 3$

Report an Error

Example Question #131 : Integral Applications

What is the average value of the function f(x) = xe^x on the interval $\left [2,3 \right ]$ ?

Possible Answers:

2e^2 -e

3e^3 -2e^2

e^2

e^3

2e^3 -e^2

Correct answer:

2e^3 -e^2

Explanation:

The average value of the function f(x) = xe^x on the interval $\left [0, 1 \right ]$ is equal to

$\frac{1}{ 3-2 }\int_{ 2}^{3} xe^x \; \mathrm{d}x$

$=\int_{ 2}^{3} xe^x \; \mathrm{d}x$

For now, we look at the indefinite integral $\int xe^x \; \mathrm{d}x$ . The integral can be changed by setting u = x and $\mathrm{d}v = e^x \mathrm{d}x$ . Then

$\frac{\mathrm{d} u}{\mathrm{d} x} = 1$ , or $\mathrm{d} u = \mathrm{d} x$

and

$v = \int e^x \mathrm{d}x = e^x$

$\int xe^x \; \mathrm{d}x$

$= \int u\; \mathrm{d} v$

$= uv -\int v\; \mathrm{d} u$

$=xe^x -\int e^x \; \mathrm{d} x$

=xe^x - e^x

which is the antiderivative.

Now, we can find the definite integral, and, subsequently, the average value:

$\int_{ 2}^{3} xe^x \; \mathrm{d}x$

$= \left.\begin{matrix} xe^x - e^x\\ \\ \end{matrix}\right| \begin{matrix} 3\\ \\ 2 \end{matrix}$

=(3e^3 - e^3) - (2e^2 - e^2) = 2e^3 -e^2

Report an Error

Example Question #313 : Integrals

Approximate the length of the curve of $f (x) = \frac{1}{4^{x}}$ on the interval [0,2] . Use Simpson's Parabolic Rule with n = 4 to make your estimate to the nearest thousandth.

Possible Answers:

2.304

1.468

2.162

1.082

2.293

Correct answer:

2.293

Explanation:

The length of the curve of f(x) on the interval [a,b] can be determined by evaluating the integral

$\int_{a}^{b} \sqrt{1 + f'(x) ^{2}} \; \mathrm{d}x$ .

$f (x) = \frac{1}{4^{x}} = e ^{ \ln \frac{1}{4} \cdot x} = e ^{ -\ln 4 \cdot x}$ , so

$f'(x) =-\ln 4 e ^{ -\ln 4 \cdot x} = - \frac{\ln 4}{4^{x}}$ , and the integral to be approximated is

$\int_{0}^{2} \sqrt{1 + \left ( - \frac{\ln 4}{4^{x}} \right ) ^{2}} \; \mathrm{d}x$ , or simplified,

$\int_{0}^{2} \sqrt{1 + \frac{\left ( \ln 4 \right )^{2}}{16^{x}} } \; \mathrm{d}x$ .

We divide the interval [0,2] into four subintervals of width $\Delta x = 2 \div 4 = 0.5$ each, so

$x_{0} = 0, x_{1} = 0.5, x_{2} = 1, x_{3} = 1.5, x_{4} = 2$ .

By Simpson's rule, we can estimate the integral by evaluating

$\frac{\Delta x}{3} \left ( g (x_{0}) + 4g(x_{1}) + 2g(x_{2}) + 4 g (x_{3}) + g (x_{4}) \right )$

$= \frac{0.5 }{3} \left ( g (0) + 4g(0.5) + 2g(1) + 4 g (1.5) + g (2) \right )$

where $g(x) = \sqrt{1 + \frac{\left ( \ln 4 \right )^{2}}{16^{x}} }$ .

We evaluate at these points, then substitute:

$g(0) = \sqrt{1 + \frac{\left ( \ln 4 \right )^{2}}{16^{0}} } = \sqrt{1 + \frac{\left ( \ln 4 \right )^{2}}{1} } \approx \sqrt{1 + \frac{\left ( 1.3863)^{2}}{1} }$

$\approx \sqrt{1 + \frac{1.9218 }{1} } \approx 1.7093$

$g(0.5) = \sqrt{1 + \frac{\left ( \ln 4 \right )^{2}}{16^{0.5}} }= \sqrt{1 + \frac{\left ( \ln 4 \right )^{2}}{4} } \approx \sqrt{1 + \frac{\left ( 1.3863)^{2}}{4} }$

$\approx \sqrt{1 + \frac{1.9218 }{4} } \approx 1.2167$

$g(1) = \sqrt{1 + \frac{\left ( \ln 4 \right )^{2}}{16^{1}} }= \sqrt{1 + \frac{\left ( \ln 4 \right )^{2}}{16 } } \approx \sqrt{1 + \frac{\left ( 1.3863)^{2}}{16} }$

$\approx \sqrt{1 + \frac{1.9218 }{16} } \approx 1.0584$

$g(1.5) = \sqrt{1 + \frac{\left ( \ln 4 \right )^{2}}{16^{1.5}} }= \sqrt{1 + \frac{\left ( \ln 4 \right )^{2}}{64} } \approx \sqrt{1 + \frac{\left ( 1.3863)^{2}}{64} }$

$\approx \sqrt{1 + \frac{1.9218 }{64} } \approx 1.0149$ $g(2) = \sqrt{1 + \frac{\left ( \ln 4 \right )^{2}}{16^{2}} } = \sqrt{1 + \frac{\left ( \ln 4 \right )^{2}}{256} } \approx \sqrt{1 + \frac{\left ( 1.3863)^{2}}{256} }$

$\approx \sqrt{1 + \frac{1.9218 }{256} } \approx 1.0037$

The approximation is therefore

$\approx \frac{0.5 }{3} \left ( 1.7093 +4 \cdot 1.2167 + 2\cdot 1.0584 +4 \cdot 1.0149 +1.0037 \right )$

$\approx \frac{0.5 }{3} \left ( 1.7093 +4.8668 + 2.1168 +4.0596 +1.0037 \right )$

$\approx \frac{0.5 }{3} \left (13.7562 \right ) \approx 2.293$

Report an Error

Example Question #132 : Integral Applications

Approximate the length of the curve of $f (x) = x^{2}+ x$ on the interval [0,2] . Use Simpson's Parabolic Rule with n = 4 to make your estimate to the nearest thousandth.

Possible Answers:

4.733

4.667

17.068

6.379

5.531

Correct answer:

6.379

Explanation:

The length of the curve of f(x) on the interval [a,b] can be determined by evaluating the integral

$\int_{a}^{b} \sqrt{1 + f'(x) ^{2}} \; \mathrm{d}x$ .

$f(x) = x^{2} + x$ , so

f'(x) =2 x + 1 , and the integral to be approximated is

$\int_{0}^{2} \sqrt{1 + \left ( 2x + 1\right ) ^{2}} \; \mathrm{d}x$

$= \int_{0}^{2} \sqrt{4x ^{2} + 4x + 2} \; \mathrm{d}x$

We divide the interval [0,2] into four subintervals of width $\Delta x = 2 \div 4 = 0.5$ each, so

$x_{0} = 0, x_{1} = 0.5, x_{2} = 1, x_{3} = 1.5, x_{4} = 2$ .

By Simpson's rule, we can estimate the integral by evaluating

$\frac{\Delta x}{3} \left ( g (x_{0}) + 4g(x_{1}) + 2g(x_{2}) + 4 g (x_{3}) + g (x_{4}) \right )$

$= \frac{0.5 }{3} \left ( g (0) + 4g(0.5) + 2g(1) + 4 g (1.5) + g (2) \right )$

where $g(x) = \sqrt{4x ^{2} + 4x + 2}$

We evaluate at these points, then substitute:

$g(0) = \sqrt{4 \cdot 0^{2} + 4\cdot 0 + 2} = \sqrt{ 2}$

$g(0.5) = \sqrt{4 \cdot 0.5^{2} + 4\cdot 0.5 + 2} = \sqrt{ 5}$

$g(1) = \sqrt{4 \cdot 1^{2} + 4\cdot 1 + 2} = \sqrt{ 10}$

$g(0.5) = \sqrt{4 \cdot 1.5^{2} + 4\cdot 1.5 + 2} = \sqrt{ 17}$

$g(2) = \sqrt{4 \cdot 2^{2} + 4\cdot 2 + 2} = \sqrt{ 26}$

The approximation is therefore

$\frac{0.5 }{3} \left ( \sqrt{2} +4 \sqrt{5} +2 \sqrt{10} +4\sqrt{17} +\sqrt{26} \right )$

$\approx \frac{0.5 }{3} \left ( 1.4142 +4 \cdot 2.2361 + 2\cdot 3.1623 +4 \cdot 4.1231 +5.0990 \right )$

$\approx \frac{0.5 }{3} \left ( 1.4142 + 8.9444 + 6.3246 +16.4924 +5.0990 \right )$

$\approx \frac{0.5 }{3} \left ( 38.2745\right ) \approx 6.379$

Report an Error

Example Question #138 : Integral Applications

What is the average value of the function f(x) = | x^2 - 4 | on the interval [0, 4] ?

Possible Answers:

$3\sqrt{2}$

$2\sqrt{2}$

$5 - \sqrt{2}$

Correct answer:

Explanation:

The average value of the function f(x) = | x^2 - 4 | on the interval [0, 4] is equal to

$\frac{1}{4-0}\int_{0}^{4} | x^2 - 4 | \; \mathrm{d}x$ , or

$\frac{1}{4 }\int_{0}^{4} | x^2 - 4 | \; \mathrm{d}x$ .

To evaluate this integral, we note that x^2 - 4 has negative value on (0, 2) and positive value on (2, 4] , so on [0,4] , f(x) can be defined as

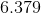
$f(x) = \left\{\begin{matrix} -\left ( x^2 - 4\right ) & x \in [0, 2) \\ x^2 - 4 & x \in \left [ 2, 4\right ] \end{matrix}\right.$

$f(x) = \left\{\begin{matrix} - x^2 + 4 & x \in [0, 2) \\ x^2 - 4 & x \in \left [ 2, 4\right ] \end{matrix}\right.$

Therefore, the average value of is equal to

$\frac{1}{4 }\left [ \int_{0}^{2}\left ( - x^2 + 4 \right ) \; \mathrm{d}x + \int_{2}^{4}\left ( x^2 - 4 \right ) \; \mathrm{d}x \right ]$

$=\frac{1}{4 }\left [ \left.\begin{matrix} \left ( - \frac{x^3}{3} + 4x \right ) \\ \\ \end{matrix}\right| \begin{matrix} 2\\ \\ 0 \end{matrix} + \left.\begin{matrix} \left ( \frac{x^3}{3} - 4x \right ) \\ \\ \end{matrix}\right| \begin{matrix} 4\\ \\ 2 \end{matrix} \right \]$

$=\frac{1}{4 }\left [ \left ( - \frac{2^3}{3} + 4 \cdot 2 \right ) - \left ( - \frac{0^3}{3} + 4 \cdot 0 \right ) + \left ( \frac{4^3}{3} - 4 \cdot 4\right ) - \left ( \frac{2^3}{3} - 4 \cdot 2 \right ) \right \]$

$=\frac{1}{4 }\left [ \left ( - \frac{8}{3} + 8 \right ) -0 + \left ( \frac{64}{3} - 16\right ) - \left ( \frac{8}{3} - 8 \right ) \right \]$

$=\frac{1}{4 }\left [ \frac{16}{3} + \frac{16}{3} - \left (- \frac{16}{3} \right ) \right \]$

$=\frac{1}{4 }\left ( \frac{16}{3} + \frac{16}{3} + \frac{16}{3} \right \) = \frac{1}{4 } \cdot16 = 4$

Report an Error

View Calculus 2 Tutors

Samita
Certified Tutor

University of Houston, Bachelor of Science, Computer Science. University of Houston, Non Degree Bachelors, Biology, General.

View Calculus 2 Tutors

Samantha
Certified Tutor

Middlesex County College, Associate in Science, Sustainability Studies.

View Calculus 2 Tutors

Satweka
Certified Tutor

The University of Texas at Dallas, Master of Science, Biomedical Engineering.

All Calculus 2 Resources

9 Diagnostic Tests 308 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Biology Tutors in Seattle, Computer Science Tutors in Chicago, Algebra Tutors in Boston, Biology Tutors in Washington DC, Algebra Tutors in New York City, ACT Tutors in Phoenix, Statistics Tutors in Miami, Algebra Tutors in Chicago, Reading Tutors in Los Angeles, Physics Tutors in San Diego

Popular Courses & Classes

ISEE Courses & Classes in San Diego, MCAT Courses & Classes in San Francisco-Bay Area, GMAT Courses & Classes in San Diego, MCAT Courses & Classes in Boston, SAT Courses & Classes in Seattle, MCAT Courses & Classes in Los Angeles, MCAT Courses & Classes in Houston, SAT Courses & Classes in Boston, LSAT Courses & Classes in Atlanta, Spanish Courses & Classes in Phoenix

Popular Test Prep

MCAT Test Prep in Seattle, MCAT Test Prep in Phoenix, ISEE Test Prep in Boston, MCAT Test Prep in San Diego, ACT Test Prep in Los Angeles, SAT Test Prep in Denver, LSAT Test Prep in Atlanta, GMAT Test Prep in San Diego, SSAT Test Prep in New York City, SAT Test Prep in Los Angeles

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Calculus 2 : Integral Applications

Study concepts, example questions & explanations for Calculus 2

All Calculus 2 Resources

Example Questions

Example Question #301 : Integrals

Example Question #1 : Length Of Curve, Distance Traveled, Accumulated Change, Motion Of Curve

Example Question #1 : Length Of Curve, Distance Traveled, Accumulated Change, Motion Of Curve

Example Question #131 : Integral Applications

Example Question #133 : Integral Applications

Example Question #131 : Integral Applications

Example Question #131 : Integral Applications

Example Question #313 : Integrals

Example Question #132 : Integral Applications

Example Question #138 : Integral Applications

All Calculus 2 Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: