Call Now to Set Up Tutoring:

(888) 888-0446

Calculus 2 : Derivatives

Study concepts, example questions & explanations for Calculus 2

Create An Account

All Calculus 2 Resources

9 Diagnostic Tests 308 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1571 : Calculus Ii

What is the derivative of f(x)=4x^3-9x^2+7x-1 ?

Possible Answers:

$f{}'(x)=12x^2-18x-7$

$f{}'(x)=12x^2-8x+7$

$f{}'(x)=12x^2-18x+7$

$f{}'(x)=12x^2+18x+7$

$f{}'(x)=x^2-18x+7$

Correct answer:

$f{}'(x)=12x^2-18x+7$

Explanation:

Recall that when taking the derivative, multiply the exponent by the coefficient in front of the x term and then also subtract one from the exponent:

f(x)=4x^3-9x^2+7x-1

$f'(x)=3\cdot 4x^{3-1}-2\cdot9x^{2-1}+1\cdot7x^{1-1}$

$f{}'(x)=12x^2-18x+7$

Recall that the derivative of a constant is just zero.

Report an Error

Example Question #1572 : Calculus Ii

What is the second derivative of f(x)=16x^2-5x+9 ?

Possible Answers:

f{}''(x)=3

f{}''(x)=32x-5

f{}''(x)=32

f{}''(x)=32x

f{}''(x)=2x

Correct answer:

f{}''(x)=32

Explanation:

Before you can take the second derivative, you must first take the first derivative. Remember to multiply the exponent by the coefficient in front of the x term and then subtract one from the exponent:

f{}'(x)=32x-5

Now, take the second derivative:

f{}''(x)=32

Report an Error

Example Question #251 : First And Second Derivatives Of Functions

Find the first and second derivative of the function.

$f(x)=e^{5x}$

Possible Answers:

$f'(x)=5e^{5x}$

$f''(x)=25e^{5x}$

$f'(x)=5e^{5x}$

$f'(x)=5xe^{5x}$

$f'(x)=e^{5x}$

$f''(x)=e^{5x}$

$f'(x)=5xe^{5x}$

$f''(x)=25x^2e^{5x}$

Correct answer:

$f'(x)=5e^{5x}$

$f''(x)=25e^{5x}$

Explanation:

To find the first and second derivatives, we use the chain rule.

F'(x)=f'(g(x))g'(x)

where F(x)=f(g(x)) .

For the first derivative we have f(x)=e^x and g(x)=5x and so

$f'(x)=e^{5x}*5=5e^{5x}$

For the second derivative we have f(x)=5e^x and g(x)=5x and so

$f''(x)=5e^{5x}*5=25e^x$

Report an Error

Example Question #1574 : Calculus Ii

Find the first and second derivative of the function.

$f(x)=x+sin\,x$

Possible Answers:

$f'(x)=1+cos\,x$

$f''(x)=-sin\,x$

f'(x)=1

f''(x)=0

f'(x)=0

$f''(x)=-sin\,x$

$f'(x)=cos\,x$

$f''(x)=sin\,x$

Correct answer:

$f'(x)=1+cos\,x$

$f''(x)=-sin\,x$

Explanation:

We find the first derivative by deriving term by term. As such,

$f'(x)=\frac{\mathrm{d} }{\mathrm{d} x}[x]+\frac{\mathrm{d} }{\mathrm{d} x}[sin\,x]=1+cos\,x$

Taking the second derivative

$f''(x)=\frac{\mathrm{d} }{\mathrm{d} x}[1]+\frac{\mathrm{d} }{\mathrm{d} x}[cos\,x]=0-sin\,x=-sin\,x$

Report an Error

Example Question #1575 : Calculus Ii

What is the first derivative of f(x)=4x^3-2x^2+x-1?

Possible Answers:

f{}'(x)=12x+1

f{}'(x)=24x-4

$f{}'(x)=12x^2-4x-1$

$f{}'(x)=12x^2-4x+1$

$f{}'(x)=12x^2-4x$

Correct answer:

$f{}'(x)=12x^2-4x+1$

Explanation:

To find the first derivative, look at each term separately.

For the first term, multiply the exponent by the coefficient ( $4\cdot3$ ) and then subtract one from the exponent to get 12x^2 .

Do the same with the next term: $2\cdot-2$ and then subtract one from the exponent to get -4x .

For the third term, the derivative is just the coefficient (1 in this case).

The derivative of a constant is 0.

Put those all together to get your answer: $f{}'(x)=12x^2-4x+1$ .

Report an Error

Example Question #1581 : Calculus Ii

Find the second derivative of f(x)=2x^4-3x^3+5x^2-1 .

Possible Answers:

$f{}''(x)=4x^2-18x+10$

$f{}''(x)=24x^2-18x$

$f{}''(x)=24x^2-18x+10$

$f{}''(x)=24x^2-18x-1$

$f{}''(x)=24x^2+10$

Correct answer:

$f{}''(x)=24x^2-18x+10$

Explanation:

Before finding the second derivative, you must find the first derivative. Remember to multiply the exponent by the coefficient and then subtract one from the exponent. Evaluate each term separately and then put all together at the end.

The first derivative is: $f{}'(x)=8x^3=9x^2+10x$ .

Now, take the derivative of the 1st derivative to find the second derivative:

$f{}''(x)=24x^2-18x+10$ .

Report an Error

Example Question #1582 : Calculus Ii

Find the first derivative of $f(x)=\frac{6x^3-8x^2}{x^2}$ .

Possible Answers:

f{}'(x)=6

$f{}'(x)=\frac{6}{x}$

$f{}'(x)=6x^2$

f{}'(x)=6x

f{}'(x)=6x+1

Correct answer:

f{}'(x)=6

Explanation:

First, chop up the fraction into 2 separate terms and simplify:

$\frac{6x^3-8x^2}{x^2}=\frac{6x^3}{x^2}-\frac{8x^2}{x^2}=6x-8$

Now, take the derivative of that expression. Remember to multiply the exponent by the coefficient and then decrease the exponent by 1:

f{}'(x)=6

Report an Error

Example Question #1583 : Calculus Ii

$\int \frac{5}{x}-1dx$

Possible Answers:

$5ln\left | x\right |-x+C$

$5ln\left | x\right |-2x+C$

$5ln\left | x\right |-x$

$5ln\left | x\right |-5x+C$

$ln\left | x\right |-x+C$

Correct answer:

$5ln\left | x\right |-x+C$

Explanation:

Integrate each term separately. When there is just an x on the denominator, the integral of that is $ln\left | x\right |$ .

Therefore, the first term integrated is:

$5ln\left | x\right |$

The second term integrated is:

Put those together to get:

$5ln\left | x\right |-x$

Because it's an indefinite integral, remember to add C at the end:

$5ln\left | x\right |-x+C$ .

Report an Error

Example Question #3 : Velocity, Speed, Acceleration

Given the velocity function

$v(x)=\int_{0}^{x^2+2x+1} z^d\sin(z^5) dz$

where is real number such that $d\in [0,1]$ , find the acceleration function

a(x) .

Possible Answers:

$a(x)=(x+1)^{d}\sin (x+1)^{10}$

$a(x)=(2x+2)^{d}(x+1)^{2d}\sin (x+1)^{10}$

$a(x)=(x^2+2x+1)^{d}\sin (x^2+2x+1)^{10}$

$a(x)=(x^2+2x+1)^{2d}\sin (x^2+2x+1)^{10}$

$a(x)=(2x+2)(x+1)^{2d}\sin (x+1)^{10}$

Correct answer:

$a(x)=(2x+2)(x+1)^{2d}\sin (x+1)^{10}$

Explanation:

We can find the acceleration function a(x) from the velocity function by taking the derivative:

a(x)=v'(x)

We can view the function

$v(x)=\int_{0}^{x^2+2x+1} z^d\sin(z^5) dz$

as the composition of the following functions

$g(x)=\int_{0}^{x} z^d\sin(z^5) dz$

h(x)=x^2+2x+1=(x+1)^2

so that v(x)=g(h(x)) . This means we use the chain rule

[g(h(x))]'=g'(h(x))h'(x)

to find the derivative. We have $g'(x)=x^d\sin x^5$ and h'(x)=2x+2 , so we have

$a(x)=v'(x)=[(x+1)^2]^d\sin [(x+1)^2]^5\cdot (2x+2)$

$=(2x+2)(x+1)^{2d}\sin (x+1)^{10}$

Report an Error

Example Question #451 : Derivatives

Define $f (x,y) = \frac{1}{x^{2}y^{2}}$ .

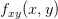
Find $f _{xy} (x,y)$ .

Possible Answers:

$f _{xy} (x,y) = - \frac{9}{x^{3}y^{3} }$

$f _{xy} (x,y) = \frac{1}{x^{3}y^{3} }$

$f _{xy} (x,y) = \frac{4}{x^{3}y^{3} }$

$f _{xy} (x,y) = \frac{9}{x^{3}y^{3} }$

$f _{xy} (x,y) = - \frac{4}{x^{3}y^{3} }$

Correct answer:

$f _{xy} (x,y) = \frac{4}{x^{3}y^{3} }$

Explanation:

First, find $f_{x} = \frac{\partial f}{\partial x}$ as follows:

$f (x,y) = \frac{1}{x^{2}y^{2}}$

$\frac{\partial }{\partial x}f (x,y) = \frac{\partial }{\partial x}\left ( \frac{1}{x^{2}y^{2}} \right )$

$=\frac{1}{ y^{2}} \cdot \frac{\partial }{\partial x}\left ( \frac{1}{x^{2} } \right )$

$=\frac{1}{ y^{2}} \cdot \frac{\partial }{\partial x}x^{-2}$

$=\frac{1}{ y^{2}} \cdot (-2) x^{-3} = -\frac{2}{x^{3}y^{2}}$

Therefore, $f_{x} (x,y ) = -\frac{2}{x^{3}y^{2}}$

Now, find $f_{xy} = \frac{\partial }{\partial y} f_{x}$ as follows:

$f_{x} (x,y ) = -\frac{2}{x^{3}y^{2}}$

$\frac{\partial }{\partial y} f_{x} (x,y ) = \frac{\partial }{\partial y}\left ( -\frac{2}{x^{3}y^{2}} \right )$

$= -\frac{2}{x^{3} } \cdot \frac{\partial }{\partial y}\left ( \frac{1}{ y^{2}} \right )$

$= -\frac{2}{x^{3} } \cdot \frac{\partial }{\partial y} y^{-2}$

$= -\frac{2}{x^{3} } \cdot (-2) y^{-3}$

$= -\frac{2}{x^{3} } \cdot \left ( -\frac{2}{y^{3} } \right )$

$= \frac{4}{x^{3}y^{3} }$

Report an Error

View Calculus 2 Tutors

Ping
Certified Tutor

The University of Texas at Dallas, Bachelor of Science, Computer Science. University of North Texas, Master of Arts, Education.

View Calculus 2 Tutors

Fatemeh
Certified Tutor

University of Isfahan, Doctor of Engineering, Chemical Engineering. University of Windsor, Doctor of Engineering, Environment...

View Calculus 2 Tutors

MEER
Certified Tutor

IIT , Master's/Graduate, Microelectronics .

All Calculus 2 Resources

9 Diagnostic Tests 308 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Biology Tutors in Miami, Biology Tutors in San Diego, Statistics Tutors in Phoenix, GRE Tutors in Seattle, GRE Tutors in New York City, French Tutors in Seattle, English Tutors in San Francisco-Bay Area, English Tutors in Los Angeles, Computer Science Tutors in Los Angeles, MCAT Tutors in Washington DC

Popular Courses & Classes

ISEE Courses & Classes in Los Angeles, ISEE Courses & Classes in Chicago, ACT Courses & Classes in Atlanta, GMAT Courses & Classes in Miami, SAT Courses & Classes in Phoenix, ISEE Courses & Classes in Phoenix, GMAT Courses & Classes in Chicago, ACT Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in Philadelphia, ISEE Courses & Classes in Dallas Fort Worth

Popular Test Prep

ISEE Test Prep in San Francisco-Bay Area, GRE Test Prep in Seattle, SAT Test Prep in Seattle, LSAT Test Prep in Washington DC, GMAT Test Prep in Denver, GRE Test Prep in San Diego, ACT Test Prep in New York City, ACT Test Prep in San Francisco-Bay Area, ISEE Test Prep in Chicago, GMAT Test Prep in Philadelphia

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Calculus 2 : Derivatives

Study concepts, example questions & explanations for Calculus 2

All Calculus 2 Resources

Example Questions

Example Question #1571 : Calculus Ii

Example Question #1572 : Calculus Ii

Example Question #251 : First And Second Derivatives Of Functions

Example Question #1574 : Calculus Ii

Example Question #1575 : Calculus Ii

Example Question #1581 : Calculus Ii

Example Question #1582 : Calculus Ii

Example Question #1583 : Calculus Ii

Example Question #3 : Velocity, Speed, Acceleration

Example Question #451 : Derivatives

All Calculus 2 Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: