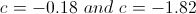Call Now to Set Up Tutoring:

(888) 888-0446

Calculus 1 : Other Points

Study concepts, example questions & explanations for Calculus 1

Create An Account

All Calculus 1 Resources

10 Diagnostic Tests 438 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Other Points

Find the critical points (rounded to two decimal places):

f(x)= x^3+3x^2+x

Possible Answers:

$c=0.18\ and\ c=1.82$

$c=-0.18\ and\ c=-1.82$

$c=-0.25\ and\ c=-2.41$

$c=0.25\ and\ c=2.41$

Correct answer:

$c=-0.18\ and\ c=-1.82$

Explanation:

To find the critical points, set f{}'(x)=0 and solve for .

f(x)= x^3+3x^2+x

Differentiate:

$f{}'(x)= 3x^2+6x+1$

Set equal to zero:

3x^2+6x+1=0

Solve for using the quadratic formula: $x= \frac{-b\pm \sqrt{b^2-4ac}}{2a}$

$a=3,\ b=6,\ c=1$

$x= \frac{-6\pm \sqrt{(6)^2-4(3)(1)}}{2(3)}$

$x= \frac{-6\pm \sqrt{36-12}}{6}}$

$x= \frac{-6+\sqrt{24}}{6}}\ and\ x= \frac{-6-\sqrt{24}}{6}}$

$c=-0.18\ and\ c=-1.82$

Report an Error

Example Question #2 : How To Graph Functions Of Points

Find the value(s) of the critical point(s) of

f(x)=x^3+2x^2+x+4 .

Possible Answers:

$\\ c_1=-3 \\ \\ c_2=1$

$\\ c_1=\frac{1}{3} \\ \\ c_2=1$

$\\ c_1=3 \\ \\ c_2=-1$

$\\ c_1=-\frac{1}{3} \\ \\ c_2=-1$

There are no real answers.

Correct answer:

$\\ c_1=-\frac{1}{3} \\ \\ c_2=-1$

Explanation:

In order to find the critical points, we must find $\ f'(x)$ and solve for $\ x$

f(x)=x^3+2x^2+x+4

$\\ \\ f'(x)=3x^2+4x+1$

Set f'(x)=0

$\\ \\ 3x^2+4x+1=0$

Use the quadratic equation to solve for $\ x$ .

Remember that the quadratic equation is as follows.

$\\ \\ x=\frac{-b\pm\sqrt{b^2-4\cdot a\cdot c}}{2\cdot a}$ , where a,b and c refer to the coefficents in the

equation ax^2+bx+c=0 .

In this case, a=3 , b=4 , and c=1 .

After plugging in those values, we get

$\\ \\ x=\frac{-4\pm\sqrt{4^2-4\cdot3\cdot1}}{2\cdot3} =\frac{-4 \pm \sqrt{4}}{6}=\frac{-4 \pm 2}{6}$ .

So the critical points values are:

$\\ \\ c_1=\frac{-4+2}{6}=\frac{-1}{3}$

$\\ \\ c_2=\frac{-4-2}{6}=-1$

Report an Error

Example Question #1 : How To Graph Functions Of Points

Find the value(s) of the critical point(s) of

f(x)=5x^3+10x^2+x+100 .

Possible Answers:

$\\ c_1=0 \\ \\ c_2=0$

$\\ c_1=\frac{-10+\sqrt{85}}{15} \\ \\ c_2=\frac{-10-\sqrt{85}}{15}$

$\\ c_1=1 \\ \\ c_2=0$

$\\ c_1=\frac{-10+\sqrt{85}}{30} \\ \\ c_2=\frac{-10-\sqrt{85}}{30}$

$\\ c_1=\frac{\sqrt{85}}{15} \\ \\ c_2=\frac{-\sqrt{85}}{15}$

Correct answer:

$\\ c_1=\frac{-10+\sqrt{85}}{15} \\ \\ c_2=\frac{-10-\sqrt{85}}{15}$

Explanation:

In order to find the critical points, we must find $\ f'(x)$ and solve for $\ x$ .

$\\ \\ f(x)=5x^3+10x^2+x+100$

$\\ \\ f'(x)=15x^2+20x+1$

Set $\ f'(x)=0$

$\\ \\ 15x^2+20x+1=0$

Use the quadratic equation to solve for $\ x$ .

Remember that the quadratic equation is as follows.

$\\ \\ x=\frac{-b\pm\sqrt{b^2-4\cdot a\cdot c}}{2\cdot a}$ , where a,b and c refer to the coefficents in the equation ax^2+bx+c=0 .

In this case, a=15 , b=20 , and c=1 .

After plugging in those values, we get.

${}\\ x=\frac{-20\pm\sqrt{20^2-4\cdot15\cdot1}}{2\cdot15} =\frac{-20 \pm \sqrt{340}}{30} \\ \\ x=\frac{-20 \pm 2\cdot\sqrt{85}}{30}$

So the critical points values are,

${}\\ \\ c_1=\frac{-20+2\cdot \sqrt{85}}{30}=\frac{-10+\sqrt{85}}{15} \\ \\ c_2=\frac{-20-2\cdot \sqrt{85}}{30}=\frac{-10-\sqrt{85}}{15}$

Report an Error

Example Question #2 : Other Points

Find the critical points of

f(x)=x^3+3x^2+x+5

Possible Answers:

$\\ c_1=-1+\frac{\sqrt{6}}{3}\\\\\ c_2=-1-\frac{\sqrt{6}}{3}$

$\\ c_1=0\\\\\ c_2=-1-\frac{\sqrt{6}}{3}$

The critical points are complex.

$\\ c_1=\frac{\sqrt{6}}{3}\\\\\ c_2=-\frac{\sqrt{6}}{3}$

Correct answer:

$\\ c_1=-1+\frac{\sqrt{6}}{3}\\\\\ c_2=-1-\frac{\sqrt{6}}{3}$

Explanation:

First we need to find f'(x) .

f(x)=x^3+3x^2+x+5

f'(x)=3x^2+6x+1

Now we set f'(x)=0.

3x^2+6x+4=0.

Now we can use the quadratic equation in order to find the critical points.

Remember that the quadratic equation is

$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$ ,

where a,b,c refer to the coefficients in the equation

ax^2+bx+c=0

In this case, a=3, b=6, and c=1.

$x=\frac{-6\pm\sqrt{(-6)^2-4(3)(1)}}{(2)(3)}$

$x=\frac{-6\pm\sqrt{24}}{6}=\frac{-6\pm2\sqrt{6}}{6}$

Thus are critical points are

$c_1=\frac{-6+2\sqrt{6}}{6}=-1+\frac{\sqrt{6}}{3}$

$c_2=\frac{-6-2\sqrt{6}}{6}=-1-\frac{\sqrt{6}}{3}$

Report an Error

Example Question #5 : Other Points

Find the critical points of

f(x)=x^2-2x+1 .

Possible Answers:

There are no critical points.

x=2

x=1

x=0

Correct answer:

x=1

Explanation:

In order to find the critical points, we need to find f'(x) using the power rule $f(x)=x^n \rightarrow f'(x)=nx^{n-1}$ .

f(x)=x^2-2x+1

f'(x)=2x-2

Now we set f'(x)=0 , and solve for .

2x-2=0

2x=2

x=1

Thus x=1 is a critical point.

Report an Error

Example Question #2 : How To Graph Functions Of Points

Find the critical point(s) of $f(x)=2x^{2}-5x+4$ .

Possible Answers:

$c=\frac{4}{5}$

$c=\frac{4}{5}$ and $c=-\frac{4}{5}$

$c=\frac{5}{4}$ and $c=-\frac{5}{4}$

$c=\frac{5}{4}$

$c=\frac{5}{4}$ and $c=-\frac{4}{5}$

Correct answer:

$c=\frac{5}{4}$

Explanation:

To find the critical point(s) of a function f(x) , take its derivative f'(x) , set it equal to , and solve for .

Given $f(x)=2x^{2}-5x+4$ , use the power rule

$f(x)=x^n \rightarrow f'(x)=nx^{n-1}$ to find the derivative. Thus the derivative is, f'(x)=4x-5=0 .

Since 4x-5=0 :

4x=5

$x=\frac{5}{4}$

The critical point is $c=\frac{5}{4}$ .

Report an Error

Example Question #2 : Other Points

Find the critical points of

f(x)=3x^3-20x^2+4x+99 .

Possible Answers:

x=0

$c=\frac{20-2\sqrt{91}}{9}$

$\\ c_1=\frac{20+2\sqrt{91}}{9} \\ \\ c_2=\frac{20-2\sqrt{91}}{9}$

There are no critical points

$\\ c=\frac{20+2\sqrt{91}}{9}$

Correct answer:

$\\ c_1=\frac{20+2\sqrt{91}}{9} \\ \\ c_2=\frac{20-2\sqrt{91}}{9}$

Explanation:

In order to find the critical points, we must find f'(x) using the power rule $f(x)=x^n \rightarrow f'(x)=nx^{n-1}$ .

f(x)=3x^3-20x^2+4x+99

f'(x)=9x^2-40x+4 .

Now we set f'(x)=0 .

9x^2-40x+4=0

Now we use the quadratic equation in order to solve for .

Remember that the quadratic equation is as follows.

$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$ ,

where a,b,c correspond to the coefficients in the equation

ax^2+bx+c=0 .

In this case, a=9, b=-40, c=4.

$x=\frac{40\pm\sqrt{(-40)^2-4(9)(4)}}{2(9)}$

$x=\frac{40\pm\sqrt{1600-144}}{18}$

$x=\frac{40\pm\sqrt{1456}}{18}=\frac{40\pm4\sqrt{91}}{18}$

Then are critical points are:

$c_1=\frac{40+4\sqrt{91}}{18}=\frac{20+2\sqrt{91}}{9}$

$c_2=\frac{40-4\sqrt{91}}{18}=\frac{20-2\sqrt{91}}{9}$

Report an Error

Example Question #2 : Other Points

Find all the critical points of

f(x)=x^3-2x+10 .

Possible Answers:

x=0

There are no critical points.

$\\ x=\sqrt{\frac{2}{3}} \\ \\ x=-\sqrt{\frac{2}{3}}$

$\\ x=\sqrt{\frac{2}{3}}$

$x=-\sqrt{\frac{2}{3}}$

Correct answer:

$\\ x=\sqrt{\frac{2}{3}} \\ \\ x=-\sqrt{\frac{2}{3}}$

Explanation:

In order to find the critical points, we first need to find f'(x) using the power rule $f(x)=x^n \rightarrow f'(x)=nx^{n-1}$ ..

f(x)=x^3-2x+10

f'(x)=3x^2-2

Now we set f'(x)=0 .

3x^2-2=0

3x^2=2

$x^2=\frac{2}{3}$

$x=\pm\sqrt{\frac{2}{3}}$

Thus the critical points are at

$x=\sqrt{\frac{2}{3}}$ , and

$x=-\sqrt{\frac{2}{3}}$ .

Report an Error

Example Question #2 : Other Points

Find the critical points of the following function:

$y=\frac{x^6}{6}+\frac{3x^5}{5}-\frac{13x^4}{4}-5x^3$

Possible Answers:

$x=\left \{ {-5, -1, 0, 3} \right \}$

$x=\left \{ {0, 1.332, 6.013} \right \}$

$x=\left \{ {{-5, -1, 0, 3}} \right \}$

$x=\left \{ {-3, 0, 1, 5} \right \}$

$x=\left \{ {-6.013, -1.332, 0} \right \}$

Correct answer:

$x=\left \{ {{-5, -1, 0, 3}} \right \}$

Explanation:

To find critical points the derivative of the function must be found.

$y=\frac{x^6}{6}+\frac{3x^5}{5}-\frac{13x^4}{4}-5x^3$

y'=x^5+3x^4-13x^3-15x^3

Critical points occur where the derivative equals zero.

0=x^5+3x^4-13x^3-15x^3

0=x^2(x+1)(x+5)(x-3)

$x=\left \{ {{-5, -1, 0, 3}} \right \}$

Report an Error

Example Question #3 : Other Points

Determine the point on the graph that is not changing if $f(x)=x^{2}-12x+32$ .

Possible Answers:

(6,-2)

(3,-2)

(0,-4)

(6,-4)

(0,0)

Correct answer:

(6,-4)

Explanation:

To find the point where the graph of f(x) is not changing, we must set the first derivative equal to zero and solve for .

To evaluate this derivate, we need the following formulae:

$\frac{d}{dx}(c)=0, \frac{d}{dx}(x)=1, \frac{d}{dx}cx=c$

$\frac{d}{dx}(x^{n}))=nx^{n-1}, \frac{d}{dx}(cx^{n})=ncx^{n-1}$

$f'(x)=2x^{2-1}-12x^{1-1}+0=2x-12$

Now, setting the derivate equal to to find where the graph is not changing:

2x-12=0 ==> x=6

Now, to find the corresponding value, we plug this value back into f(x) :

$f(6)=6^{2}-12(6)+32=36-72+32=-4$

Therefore, the point where f(x) is not changing is (6,-4)

Report an Error

View Calculus Tutors

Giles
Certified Tutor

Fourah Bay College, University of Sierra Leone, Bachelor in Arts, Physics.

View Calculus Tutors

Satweka
Certified Tutor

The University of Texas at Dallas, Master of Science, Biomedical Engineering.

View Calculus Tutors

Mark
Certified Tutor

University of Washington, Bachelor in Arts, Music Theory and Composition.

All Calculus 1 Resources

10 Diagnostic Tests 438 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Math Tutors in Phoenix, French Tutors in San Diego, SSAT Tutors in San Diego, English Tutors in Chicago, SAT Tutors in Boston, Chemistry Tutors in Miami, Math Tutors in Chicago, Algebra Tutors in San Francisco-Bay Area, LSAT Tutors in Philadelphia, ISEE Tutors in Washington DC

Popular Courses & Classes

MCAT Courses & Classes in San Diego, ACT Courses & Classes in Washington DC, ACT Courses & Classes in Boston, Spanish Courses & Classes in Houston, ACT Courses & Classes in Seattle, ACT Courses & Classes in Atlanta, Spanish Courses & Classes in Chicago, GRE Courses & Classes in Philadelphia, SAT Courses & Classes in New York City, SSAT Courses & Classes in San Francisco-Bay Area

Popular Test Prep

ACT Test Prep in Washington DC, ISEE Test Prep in Houston, ACT Test Prep in Atlanta, LSAT Test Prep in Dallas Fort Worth, ISEE Test Prep in Chicago, SAT Test Prep in Dallas Fort Worth, SAT Test Prep in Houston, LSAT Test Prep in Chicago, GMAT Test Prep in Miami, SAT Test Prep in Denver

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Calculus 1 : Other Points

Study concepts, example questions & explanations for Calculus 1

All Calculus 1 Resources

Example Questions

Example Question #1 : Other Points

Example Question #2 : How To Graph Functions Of Points

Example Question #1 : How To Graph Functions Of Points

Example Question #2 : Other Points

Example Question #5 : Other Points

Example Question #2 : How To Graph Functions Of Points

Example Question #2 : Other Points

Example Question #2 : Other Points

Example Question #2 : Other Points

Example Question #3 : Other Points

All Calculus 1 Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: