All Calculus 1 Resources
Example Questions
Example Question #121 : How To Find Acceleration
A snowball rolls into a valley. Its position is represented by 


What is the acceleration of the snowball?
Take the second derivative, using the Power Rule (

Example Question #121 : Acceleration
A weight hanging from a spring is stretched down 3 units beyond its rest position and released at time 

What is the acceleration at time 
Example Question #123 : How To Find Acceleration
The position of a particle is given by the expression

At what time 

To find the acceleration of a particle given the equation for position x(t), utilize the relationship
Therefore, to find the acceleration, we take the second derivative of x(t):
Now to find where the acceleration is 30, we set 6t equal to 30 and solve for t:
Which gives us the correct answer.
Example Question #124 : How To Find Acceleration
The velocity of a particle is given by the equation

To two decimal places, what is the acceleration of the particle at 
The acceleration of a particle is given by the first derivative of the velocity:
Here, the chain rule must be used to fine the derivative of the velocity:
Finally, evaluate the expression for acceleration at t=3:
Example Question #125 : How To Find Acceleration
Find 


In order to evaluate at 

We found this by using the definition of derivatives for exponential functions and the product rule.
Remember that the definition of derivaties for exponential functions are

Remember that the product rule is as follows:
Now lets find 
Now lets evaluate 
Example Question #126 : How To Find Acceleration
Find the acceleration of a particle at 

Acceleration of a particle is given by the second derivative of the position function. The position function is
Taking the first derivative gives the velocity function:
Taking the second derivative gives the acceleration function:
Evaluating the function at 
Example Question #127 : How To Find Acceleration
A given ball has a position defined by the equation 

Acceleration is defined as the second derivative of position, or 
According to the Power Rule, the first derivative


therefore, the second derivative


Applying this to



Plugging in 

Example Question #128 : How To Find Acceleration
A given propeller plane has a position defined by the equation 

Acceleration is defined as the second derivative of position, or 
According to the Power Rule, the first derivative


therefore, the second derivative


Applying this to



Plugging in 

Example Question #129 : How To Find Acceleration
A given object has a position defined by the equation 

Acceleration is defined as the second derivative of position, or 
According to the Power Rule, the first derivative


therefore, the second derivative


Applying this to



Plugging in 

Example Question #130 : How To Find Acceleration
If the position of particle is 

Since the acceleration is the second derivative of the position 
So the acceleration function is 
All Calculus 1 Resources












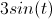

























![[f(x)g(x)]'=f'(x)g(x)+f(x)g'(x)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/372321/gif.latex)





































