All Calculus 1 Resources
Example Questions
Example Question #4 : How To Find Increasing Intervals By Graphing Functions
Is the following function increasing or decreasing on the interval ![[2,3]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/325776/gif.latex)
Decreasing, because 
Increasing, because 
The function is neither increasing nor decreasing on the interval.
Decreasing, because 
Increasing, because 
Increasing, because 
A function is increasing on an interval if for every point on that interval the first derivative is positive.
So we need to find the first derivative and then plug in the endpoints of our interval.
Find the first derivative by using the Power Rule
Plug in the endpoints and evaluate the function.
Both are positive, so our function is increasing on the given interval.
Example Question #2 : Increasing Intervals
On which intervals is the following function increasing?
The first step is to find the first derivative.
Remember that the derivative of
Next, find the critical points, which are the points where 




The final step is to try points in all the regions 

If we plugin in a number from the first range, i.e 
From the second range, 
From the third range, 
From the last range, 
So the second and the last ranges are the ones where 
Example Question #8 : How To Find Increasing Intervals By Graphing Functions
Below is the complete graph of 

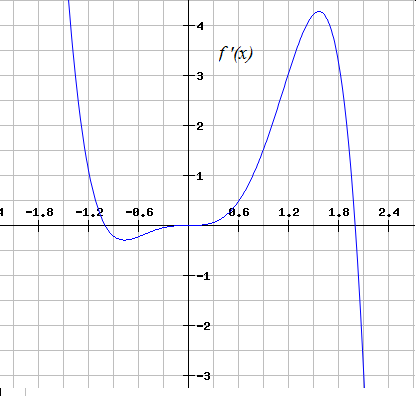




Example Question #9 : How To Find Increasing Intervals By Graphing Functions
Function A
Function B
Function C
Function D
Function E
5 graphs of different functions are shown above. Which graph shows an increasing/non-decreasing function?
Function A
Function E
Function D
Function C
Function B
Function E
A function 


Function E is the only function that has this property. Note that function E is increasing, but not strictly increasing
Example Question #5 : How To Find Increasing Intervals By Graphing Functions
Find the increasing intervals of the following function on the interval 
To find the increasing intervals of a given function, one must determine the intervals where the function has a positive first derivative. To find these intervals, first find the critical values, or the points at which the first derivative of the function is equal to zero.
For the given function, 
This derivative was found by using the power rule

When set equal to zero, 





Example Question #31 : Intervals
Is 

f(x) is flat at the point, because f'(x) is zero.
f(x) is decreasing at the point, because f'(x) is negative.
f(x) is decreasing at the point, because f'(x) is positive.
f(x) is increasing at the point, because f'(x) is positive.
f(x) is decreasing at the point, because f'(x) is negative.
Is f(x) increasing, decreasing, or flat at 
Recall that to find if a function is increasing or decreasing, we can use its first derivative. If f'(x) is positive, f(x) is increasing. If f'(x) is negative, f(x) is decreasing.
So, given:
We get
Then:
Therefore, f(x) is decreasing at the point, because f'(x) is negative.
Example Question #32 : Intervals
Tell whether 
![[4,7]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/384983/gif.latex)
Decreasing, because g'(t) is positive.
Increasing, because g'(t) is positive.
Decreasing, because g'(t) is negative.
Increasing, because g'(t) is negative.
Increasing, because g'(t) is positive.
Tell whether g(t) is increasing or decreasing on the interval [4,7]
To find increasing and decreasing, find where the first derivative is positive and negative. If g'(t) is positive, then g(t) is increasing and vice-versa.
Then,plug in the endpoints of [4,7] and see what you get for a sign.
So, since g'(t) is positive on the interval, g(t) is increasing.
Example Question #13 : Increasing Intervals
Find the interval on which the function is increasing:
The function is never increasing.
To find the interval(s) on which the function is increasing, we must find the intervals on which the first derivative of the function is positive.
The first derivative of the function is:
and was found using the rule
Now we must find the critical value, at which the first derivative is equal to zero:
Now, we make the intervals on which we look at the sign of the first derivative:
On the first interval the first derivative is positive, while on the second it is negative. Thus, the first interval is our answer, because over this range of x values, the first derivative is positive and the function is increasing.
Example Question #14 : Increasing Intervals
Suppose 







If 





Example Question #15 : Increasing Intervals
Deletable Note to the admin: I am virtually 100% sure the derivative has been correct. Derivative of the top is 6x. Derivative of the bottom is 1/x. So numerator of derivative by quotient rule is 
Let 


Every nontrivial subinterval of
No subinterval of 
Only intervals where 
Every nontrivial subinterval of
Take the first derivative of 






is positive for all positive 


NOTE: Interestingly the opposite of the choice 








Certified Tutor
All Calculus 1 Resources

























































