To find the velocity of the toy car, we take the derivative of the position equation. The velocity equation is

\(\displaystyle v(t) = 2t - 5\)

Then we insert \(\displaystyle t = 2\) seconds to find the instantaneous velocity.  A negative instantaneous velocity mean that the toy is slowing down.  

Solving for dv/dt, requires use of the chain rule:

\(\displaystyle \frac{dv}{dt}=\frac{dv}{dx}\frac{dx}{dt}=\frac{d}{dx}[\sin(2x)]\frac{d}{dt}[2t^2-5t+9]\)

\(\displaystyle \frac{dv}{dt}=(2\cos(2x))(4t-5)=(4t-5)(2\cos(2(2t^2-5t+9)))\)

\(\displaystyle \frac{dv}{dt}=(8t-10)\cos(4t^2-10t+18)\)

This is one of the answer choices.

If you plug \(\displaystyle 1\) into the equation, you get \(\displaystyle \frac{0}{0}\), meaning you should use L'Hopital's Rule to find the limit.

L'Hopital's Rule states that if 

 and that if 

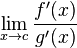 exists,

then 

In this case:

\(\displaystyle f(x) = 6x^2 -7x+1\)

\(\displaystyle g(x) = x^3-1\)

Start by finding the derivative of the numerator and evaluating it at \(\displaystyle 1\):

\(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}6x^2-7x + 1=12x-7=5\)

Do the same for the denominator:

\(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}x^3-1 = 3x^2 = 3\)

The limit is then equal to the derivative of the numerator evaluated at \(\displaystyle 1\) divided by the derivative of the denominator evaluated at \(\displaystyle 1\), or \(\displaystyle \frac{5}{3}\).

To find the slope, we need to differentiate the given function. By product rule and chain rule, we have \(\displaystyle y' = 2 \cos (2x) \cdot x^2 + \sin (2x) \cdot (2x).\) \(\displaystyle \Rightarrow y'(\frac{\pi}{2}) = 2 \cos {\pi} \cdot \frac{\pi^2}{4} + \sin \pi \cdot \pi \\ = 2 \cdot (-1) \cdot \frac{\pi^2}{4} + 0 \cdot \pi = - \frac{\pi^2}{2} .\)

You could think of a function as a machine that takes in some number, performs an operation on it, and then spits out another number

For any value of \(\displaystyle x\) in \(\displaystyle y^{2}=x+1\), there will be two values of \(\displaystyle y\).  So it is not a function.

Piecewise functions are a special type function in which the formula changes for different \(\displaystyle x\) values.

\(\displaystyle \ln(x)\) is defined when \(\displaystyle x>0\), and \(\displaystyle \sqrt {x^2-1}\) is defined when \(\displaystyle x^2-1 \geq 0\). Since the radical part is in the denominator, it cannot be \(\displaystyle 0\). Therefore, we need \(\displaystyle x^2 -1 >0 \Rightarrow x>1 \or \ x< -1.\) Combining this domain with \(\displaystyle x>0\), we get \(\displaystyle x>1\). 

To find the slope of a curve at a certain point, you must first find the derivative of that curve. 

The derivative of this curve is \(\displaystyle f'(x)=9x^{2}-7\).

Then, plug in \(\displaystyle 2\) for \(\displaystyle x\) into the derivative and you will get \(\displaystyle 151\) as the slope of \(\displaystyle f(x)\) at \(\displaystyle x=2\).

To find the critical points of a function, you need to first find the derivative and then set that equal to 0. To find the derivative, multiply the exponent by the leading coefficient and then subtract 1 from the exponent. Therefore, the derivative is \(\displaystyle f{}'(x)=3x^2-4x+1\). Set that equal to 0 and then factor so that you get: \(\displaystyle (3x-1)(x-1)=0\). Solve for x in both expressions so that your answer is: \(\displaystyle x=\frac{1}{3}, 1\).