All Basic Geometry Resources
Example Questions
Example Question #191 : Triangles
In the figure, a right isosceles triangle is placed in a rectangle. What is the area of the shaded region?


In order to find the area of the shaded region, we need to first find the areas of the triangle and the rectangle.
First, recall how to find the area of a triangle.
In the figure, we are given the triangle’s hypotenuse, which is also the width of the rectangle. We can then use this information and the Pythagorean theorem to find the length of the sides of the triangle.
Now, because this is a right isosceles triangle,
We can then make the following substitution:
Therefore:
Substitute in the value of the hypotenuse to find the length of the base:
Now, substitute this number in to find the area of the triangle.
Next, recall how to find the area of the rectangle:
Substitute in the given information from the question to find the area.
Now that we have the areas of both the rectangle and the triangle, we can find the area of the shaded region.
Solve.
Example Question #192 : Triangles
In the figure, a right isosceles triangle is placed in a rectangle. What is the area of the shaded region?


In order to find the area of the shaded region, we need to first find the areas of the triangle and the rectangle.
First, recall how to find the area of a triangle.
In the figure, we are given the triangle’s hypotenuse, which is also the width of the rectangle. We can then use this information and the Pythagorean theorem to find the length of the sides of the triangle.
Now, because this is a right isosceles triangle,
We can then make the following substitution:
Therefore:
Substitute in the value of the hypotenuse to find the length of the base:
Now, substitute this number in to find the area of the triangle.
Next, recall how to find the area of the rectangle:
Substitute in the given information from the question to find the area.
Now that we have the areas of both the rectangle and the triangle, we can find the area of the shaded region.
Solve.
Example Question #193 : Triangles
In the figure, a right isosceles triangle is placed in a rectangle. What is the area of the shaded region?


In order to find the area of the shaded region, we need to first find the areas of the triangle and the rectangle.
First, recall how to find the area of a triangle.
In the figure, we are given the triangle’s hypotenuse, which is also the width of the rectangle. We can then use this information and the Pythagorean theorem to find the length of the sides of the triangle.
Now, because this is a right isosceles triangle,
We can then make the following substitution:
Therefore:
Substitute in the value of the hypotenuse to find the length of the base:
Now, substitute this number in to find the area of the triangle.
Next, recall how to find the area of the rectangle:
Substitute in the given information from the question to find the area.
Now that we have the areas of both the rectangle and the triangle, we can find the area of the shaded region.
Solve.
Example Question #1172 : Basic Geometry
If the length of one leg of a right isosceles triangle is 16cm, what is the length of the other leg?
First we need to know that a right isosceles triangle has two legs with the same length.
In this case we do not need to worry about the hypotenuse.
Since one leg measures 16 cm, the other leg is the same length and so our answer is 16cm.
Example Question #1 : How To Find If Right Triangles Are Similar




Find 
Since 







Because the two are similar triangles, 

Therefore, 
Example Question #2 : How To Find If Right Triangles Are Similar
Which of the following is sufficient to say that two right triangles are similar?
All the angles are congruent.
Two angles and one side are congruent.
Two sides and one angle are congruent.
Two of the sides are the same.
All the angles are congruent.
If all three angles of a triangle are congruent but the sides are not, then one of the triangles is a scaled up version of the other. When this happens the proportions between the sides still remains unchanged which is the criteria for similarity.
Example Question #191 : Triangles
Which of the following statements is true regarding the two triangles?
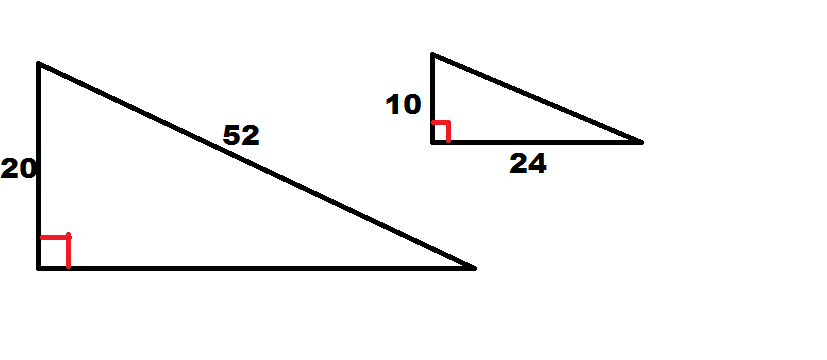
The triangles are similar by Hypotenuse-Leg
The triangles are similar because they are both right triangles.
The triangles are not similar because they are not the same size.
We do not have enough information to show the triangles are similar.
The triangles are similar by Side-Angle-Side
The triangles are similar by Side-Angle-Side
Though we must do a little work, we can show these triangles are similar. First, right triangles are not necessarily always similar. They must meet the necessary criteria like any other triangles; furthermore, there is no Hypotenuse-Leg Theorem for similarity, only for congruence; therefore, we can eliminate two answer choices.
However, we can use the Pythagorean Theorem with the smaller triangle to find the missing leg. Doing so gives us a length of 48. Comparing the ratio of the shorter legs in each trangle to the ratio of the longer legs we get
In both cases, the leg of the larger triangle is twice as long as the corresponding leg in the smaller triangle. Given that the angle between the two legs is a right angle in each triangle, these angles are congruent. We now have enough evidence to conclude similarity by Side-Angle-Side.
Example Question #192 : Triangles
Two triangles, 

Their corresponding angles are equal AND their corresponding lengths are equal.
Their corresponding angles are equal AND their corresponding lengths are proportional.
Their corresponding lengths are proportional.
Their corresponding angles are equal.
Their corresponding angles are equal AND their corresponding lengths are proportional.
The Similar Figures Theorem holds that similar figures have both equal corresponding angles and proportional corresponding lengths. Either condition alone is not sufficient. If two figures have both equal corresponding angles and equal corresponding lengths then they are congruent, not similar.
Example Question #2 : How To Find If Right Triangles Are Similar



Are 

There is not enough information given to answer this question.
Yes, because 

No, because 

Yes, because 

There is not enough information given to answer this question.
The Similar Figures Theorem holds that similar figures have both equal corresponding angles and proportional corresponding lengths. In other words, we need to know both the measures of the corresponding angles and the lengths of the corresponding sides. In this case, we know only the measures of 

It's not enough to know that both figures are right triangles, nor can we assume that angles are the same measurement because they appear to be.
Similar triangles do not have to be the same size.
Example Question #3 : How To Find If Right Triangles Are Similar



What is the length of 
Since 












Substitute the known values.
Cross-multiply and simplify.





All Basic Geometry Resources



















































































