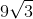To find the area of a triangle, multiply the base by the height, then divide by 2.

To find the area of a right triangle, use the formula , where  is the area of the triangle,  is the length of the triangle's base, and  is the triangle's height.

The area of a triangle is denoted by the equation 1/2 b x h.

b stands for the length of the base, and h stands for the height.

Here we are told that the perimeter (total length of all three sides) is 12, and the hypotenuse (the side that is neither the height nor the base) is 5 units long.

So, 12-5 = 7 for the total perimeter of the base and height.

7 does not divide cleanly by two, but it does break down into 3 and 4,

and 1/2 (3x4) yields 6.

Another way to solve this would be if you recall your rules for right triangles, one of the very basic ones is the 3,4,5 triangle, which is exactly what we have here

We can model the side lengths of the triangle as 3x, 4x, and 5x. We know that perimeter is 3x+4x+5x=48, which implies that x=4. This tells us that the legs of the right triangle are 3x=12 and 4x=16, therefore the area is A=1/2 bh=(1/2)(12)(16)=96.

The base is equal to 6.

The height of an quilateral triangle is equal to , where is the length of the base.

The equation used to find the area of a right triangle is:  where A is the area, b is the base, and h is the height of the triangle. In this question, we are given the height, so we need to figure out the base in order to find the area. Since we know both the height and hypotenuse of the triangle, the quickest way to finding the base is using the pythagorean theorem,  . a = the height, b = the base, and c = the hypotenuse.

Using the given information, we can write . Solving for b, we get  or . Now that we have both the base and height, we can solve the original equation for the area of the triangle. 

The area of a triangle is . For a right triangle, we can use the two legs as the base and the height regardless of orientation. Right now we only know one of the legs, and we can solve for the other using Pythagorean Theorem:

subtract 16 from both sides

we can see that all of the answers are in radical form, so we do not have to simplify this to a crazy decimal.

Now we have our "base" and "height" and we can plug them into the formula to find the area:

half of 4 is 2, so our answer is , which we can't simplify any more.

The area of a triangle is found using the formula . For a right triangle, we can use the two legs as the base and height regardless of the orientation of the triangle.

In this case, we only know one leg, but we can figure out the other by using the Pythagorean Theorem:

subtract 36 from both sides

take the square root

Now that we have our "base" and "height," we can substitute them into the formula and find the area:

To find area of this triangle, you must use the formula indicated below.

where  is base and  is height. Thus: