Call Now to Set Up Tutoring:

(888) 888-0446

Basic Geometry : Diameter

Study concepts, example questions & explanations for Basic Geometry

Create An Account

All Basic Geometry Resources

9 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #362 : Circles

The area of a circle is $196\pi$ inches^2 . What is the diameter?

Possible Answers:

$32\ in$

$14\ in$

$16\ in$

$28\ in$

$22\ in$

Correct answer:

$28\ in$

Explanation:

To find the diameter, we must first find the radius using the formula to find a circle's area.

$\pi r^2=area$

We have the area, so we have to work backwards.

$\pi r^2=196\pi$

Divide both sides by $\pi$

r^2=196

Take the square root of both sides.

$\sqrt{r^2}=\sqrt{196}$

r=14 inches

Now, since you have the radius, you have to double it to get the diameter.

diameter = 28 inches

Report an Error

Example Question #61 : Diameter

The area of a circle is $81 \pi \enspace un^2$ . What is the diameter?

Possible Answers:

4.5 un

81 un

9 un

18 un

Correct answer:

18 un

Explanation:

The area of a circle is $\pi r^2$ , which means that in this circle, the radius squared is 81. The square root of 81 is 9, which means that the radius is 9. The diameter is just twice the length of the radius, so in this case 9 times 2, which is 18.

Report an Error

Example Question #62 : Diameter

The area of a circle is $25 \pi \enspace in^2$ . What is the length of its diameter?

Possible Answers:

2.5 in

25 in

5 in

50 in

10 in

Correct answer:

10 in

Explanation:

The area of a circle is $\pi r^2$ . In this case, r ^2 = 25 . Taking the square root, the radius has a length of 5. To find the diameter, multiply by 2. Two times five is 10, so the diameter has a length of 10.

Report an Error

Example Question #365 : Circles

True or false: A circle with radius 20 has diameter 10.

Possible Answers:

True

False

Correct answer:

False

Explanation:

The diameter of a circle is twice its radius (not the other way around), so a circle with radius 20 has diameter $2 \times 20 = 40$ .

Report an Error

Example Question #364 : Basic Geometry

True or false: A circle with radius 500 centimeters has diameter one meter.

Possible Answers:

False

True

Correct answer:

False

Explanation:

The diameter of a circle is twice that of the radius, so the diameter of a circle with radius 500 centimeters is $500 \textrm{ cm} \times 2 = 1,000 \textrm{ cm}$ . However, one meter is equal to 100 centimeters, so the statement is false.

Report an Error

Example Question #371 : Basic Geometry

Use 3.14 for Pi in the following question.

If the circumference of a circle is 25.12cm, what is the measure of its diameter?

Possible Answers:

$12.5\text{ cm}$

$11.3\text{ cm}$

$8\text{ cm}$

$6\text{ cm}$

$21.98\text{ cm}$

Correct answer:

$8\text{ cm}$

Explanation:

First we need to know that the formula for circumference of a circle is

$\text{Circumference}=\text{Diameter}\cdot \pi$ .

Since we know the circumference, we can plug it into our equation, along with pi, and solve for diameter.

$25.12cm=D\cdot3.14$

To solve for D (diameter) we must divide both sides by pi

$25.12cm\div3.14=D$

when we divide 25.12 by 3.14 we get 8, so our final answer is 8cm.

Report an Error

Example Question #372 : Basic Geometry

A circular pizza has an area of $36\pi$ square inches. What is its diameter in inches?

Possible Answers:

Correct answer:

Explanation:

The area of a circle with a given radius is $A=\pi r^2$ . Since the area of the circular pizza is given as $36\pi$ square inches, we can solve for its radius as follows:

$36\pi=\pi r^2$

$\Rightarrow 36 = r^2$

$\Rightarrow r = \sqrt{36} = 6$

Now that we know that the radius of the pizza is inches, we can now deduce its diameter knowing that the diameter of a circle is equal to twice its radius. Hence, the diameter of this pizza is 2(6)=12 inches.

Report an Error

Example Question #1 : How To Find The Ratio Of Diameter And Circumference

Let represent the area of a circle and represent its circumference. Which of the following equations expresses in terms of ?

Possible Answers:

C^2

Correct answer:

Explanation:

The formula for the area of a circle is $A=\pi r^2$ , and the formula for circumference is $C=2\pi r$ . If we solve for C in terms of r, we get
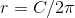
$r=C/2\pi$ .

We can then substitute this value of r into the formula for the area:

$A=\pi r^2$

$=\pi (C/2\pi )^2$

$=C^2\pi /4\pi ^2$

$=C^2/4\pi$

Report an Error

Example Question #1 : How To Find The Ratio Of Diameter And Circumference

A can of soup has a base area of $16\pi$ . What is the ratio of the can's diameter to its circumference?

Possible Answers:

$\frac{1}{2\pi}$

$\frac{1}{\pi}$

$\frac{\pi}{8}$

$\frac{\pi}{1}$

$\frac{2\pi}{1}$

Correct answer:

$\frac{1}{\pi}$

Explanation:

If the cirlcle has an area of $16\pi$ then we need to find a way to determine the diameter of the circle. We must do 4 things:

1. Find the radius of the circle since all we know is the area of the circle.

2. Double the radius to find the diameter.

3. Find the circumference by $C=\pi d$

4. Write the ratio

$A_{circle}=\pi r^2$

$16\pi=\pi r^2$

Solving to find the radius we get:

16=r^2

4=r

So if the radius is 4 then the diameter is:

d=2(4)=8

Then the circumference is:

$C=8\pi$

The ratio of the diameter to the circumference is:

$\frac{d}{C}=\frac{8}{8\pi}=\frac{1}{\pi}$

Report an Error

Example Question #2 : How To Find The Ratio Of Diameter And Circumference

The circumference of the base of a silo is $144\pi$ ft. What is the ratio of the silo's circumference to its diameter?

Possible Answers:

1:144

$144:\pi$

144:1

$\pi:1$

$1:\pi$

Correct answer:

$\pi:1$

Explanation:

Since the silo has base circumference of $144\pi$ , then according to the formula for the circumference of a circle:

$C=\pi d$

$144\pi=\pi d$

Solving for diameter:

144=d

So the diameter is 144 ft. Therefore the ratio of the circumference to the diameter would be:

$144\pi:144\rightarrow \pi:1$

Report an Error

View Tutors

Denys
Certified Tutor

Lviv National University Ukraine, Bachelors, Biology/Biophysics. University of Szeged Hungary, PHD, Computational Biophysics.

View Tutors

Abdullah
Certified Tutor

Ontario Tech University, Bachelor of Science, Mechanical Engineering.

View Tutors

Nicholas
Certified Tutor

University of California-San Diego, Bachelor of Science, Applied Mathematics.

All Basic Geometry Resources

9 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Reading Tutors in Chicago, Chemistry Tutors in Atlanta, Calculus Tutors in Denver, Reading Tutors in New York City, SSAT Tutors in Atlanta, Reading Tutors in Denver, MCAT Tutors in San Francisco-Bay Area, English Tutors in Washington DC, Physics Tutors in Dallas Fort Worth, Biology Tutors in San Diego

Popular Courses & Classes

SSAT Courses & Classes in Chicago, GMAT Courses & Classes in Atlanta, GMAT Courses & Classes in Phoenix, Spanish Courses & Classes in Chicago, SAT Courses & Classes in Chicago, ISEE Courses & Classes in New York City, MCAT Courses & Classes in Chicago, Spanish Courses & Classes in Washington DC, ISEE Courses & Classes in Los Angeles, GMAT Courses & Classes in Houston

Popular Test Prep

GMAT Test Prep in Houston, SAT Test Prep in San Francisco-Bay Area, SSAT Test Prep in Miami, SAT Test Prep in San Diego, GMAT Test Prep in Atlanta, ISEE Test Prep in San Francisco-Bay Area, GMAT Test Prep in Dallas Fort Worth, MCAT Test Prep in Chicago, SAT Test Prep in Washington DC, GRE Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Basic Geometry : Diameter

Study concepts, example questions & explanations for Basic Geometry

All Basic Geometry Resources

Example Questions

Example Question #362 : Circles

Example Question #61 : Diameter

Example Question #62 : Diameter

Example Question #365 : Circles

Example Question #364 : Basic Geometry

Example Question #371 : Basic Geometry

Example Question #372 : Basic Geometry

Example Question #1 : How To Find The Ratio Of Diameter And Circumference

Example Question #1 : How To Find The Ratio Of Diameter And Circumference

Example Question #2 : How To Find The Ratio Of Diameter And Circumference

All Basic Geometry Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: