All Basic Geometry Resources
Example Questions
Example Question #52 : How To Find The Length Of The Side Of A Square
True or false: A square with diagonals of length 2 has sides of length 
False
True
True
A square is shown below with its diagonal of length 2.
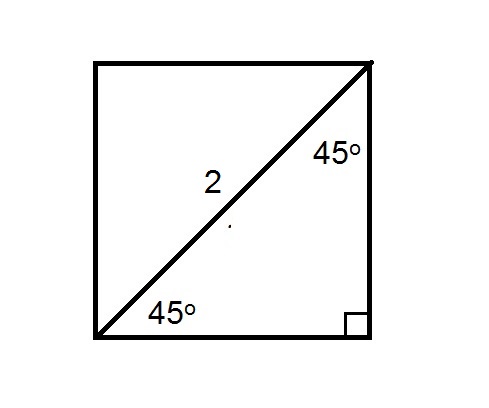
Each of the triangles formed is an isosceles right triangle with congruent legs - by the 45-45-90 Triangle Theorem, they are 45-45-90 triangles. Also by the 45-45-90 Triangle Theorem, the diagonal, each leg of the triangle has length equal to the hypotenuse divided by 


Rationalize the denominator by multiplying both halves of the fraction by 
Example Question #325 : Squares
True or false: A square with area 49 has sides of length 7.
False
True
True
Given the length of each side of a square, the area of the square is the square of this length. Therefore, to find the sidelength, take the square root of the area. The area of the square is 49, and 

Example Question #574 : Quadrilaterals
If the area of a square is 
If we are given the area of a square, in order to find the length of a side we must take the square root of the area. We need to know that the formula for area of a square is

(where s is side) so we plug in 400 for the area and we have

To solve for s we must take the square root of both sides

and we get
When taking square roots we reject the negative if we are working with measurements. Our final answer is 20 inches.
Example Question #1 : How To Find The Length Of The Hypotenuse Of A 45/45/90 Right Isosceles Triangle : Pythagorean Theorem
What is the length of the diagonal of a square with sides of 
The diagonal cuts a square into two 
Using Pythagorean Theorem we get:

Example Question #1 : How To Find The Length Of The Hypotenuse Of A 45/45/90 Right Isosceles Triangle : Pythagorean Theorem

Example Question #2 : 45/45/90 Right Isosceles Triangles
A right triangle has two sides of length 

The Pythagorean Theorem states that the sum of the squares of the sides of the triangle are equal to the square of the hypotenuse, summed up as 

which simplifies to

Example Question #1 : Triangles



Using the Pythagorean Theorem, calculate the length of the hypotenuse of 
There is not enough information given to answer this question.
The Pythagorean Theorem holds that, in a right triangle, the square of the hypotenuse equals the sum of the squares of the other two sides. That is,
where 


Here, 





Apply the Pythagorean Theorem.
So the length of the hypotenuse is 
Example Question #1 : Triangles
The following image is not to scale.
Find the length of the hypotenuse of the right triangle:
Because the problem states that this the triangle is a right triangle and provides the length of the two legs, the third side (hypotenuse) can be calculated using the Pythagorean Theorem.


Example Question #2 : How To Find The Length Of The Hypotenuse Of A 45/45/90 Right Isosceles Triangle : Pythagorean Theorem
The following image is not to scale.
Find the length of the hypotenuse of the 
45/45/90 triangles are always isosceles. This means that two of the legs of the triangle are congruent. In the figure, it's indicates which two sides are congruent.
From here, we can find the length of the hypotenuse through the Pythagorean Theorem. We can confirm this because the problem has given us no angle measures to perform trig functions with.

c also equals -2√2, but because the hypotenuse is a physical length, the value cannot be negative distance.
Example Question #2 : Triangles
Square 

Cannot be determined from the information provided
The answer can be found two different ways. The first step is to realize that this is really a triangle question, even though it starts with a square. By drawing the square out and adding the diagonal, you can see that you form two right triangles. Furthermore, the diagonal bisects two ninety-degree angles, thereby making the resulting triangles a 
From here you can go one of two ways: using the Pythagorean Theorem to find the diagonal, or recognizing the triangle as a 
1) Using the Pythagorean Theorem
Once you recognize the right triangle in this question, you can begin to use the Pythagorean Theorem. Remember the formula: 



In this case, 

The length of the diagonal is 
2) Using Properties of 
The second approach relies on recognizing a 




In this case, 
Therefore, using the 

All Basic Geometry Resources












































































