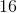The mean is the same as the average. To find the mean, use the following formula:

The mean is the same as the average. To find the mean, use the following formula:

Find the mean of the following set of numbers:

Finding the mean of a number set is essentially finding the average.

Begin by summing the numbers, then divide by the total number of terms.

Now, since there are 12 terms in the series, divide by 12

So our mean is 104.5

Find the mean of the following data set:

Whenever we are working with a data set, it can be helpful to put the terms in order:

Now that our terms are in order, we can do all sorts of things with them.

In this case, we need to find the mean. This is essentially the same as the average. 

Begin by finding the sum of our terms.

Now, because we have ten terms, we need to divide by 10

The course grade average is calculated by using Sally's three test scores and final exam. student must score at least an average of ; therefore we can write the following:

Given that the average is calculated using three test scores and a final weighted as two regular tests, we can write the following equation. 

Let's use these equations to construct an inequality where we will substitute in our known values and let a variable, , equal the final score needed to earn an a  or above.

Sally needs to at least score a  on the final to score  or above.

To find the average, add up all the values you are given and divide by the number of values there are.

18 + 12 + 22 + 24 + 14 = 90, the sum of her total points.

And 90/5 = 18, which is her average.

If you reorganize the numbers and put them in ascending order, you get:

 .

The median is the number which falls in the middle of a set. Our set has  entries therefore to find the true middle of the set we will need to take entry five and six and find its mean. We do this by adding entry five and entry six together and then dividing by two:

Therefore the median of our set is .

To solve this problem, we need to remember the definitions of mean, median, and mode:

Mean is the average of all numbers of a given set: we find this by adding all the numbers together and dividing by the total number of numbers there are.

Median is the middle of a data set: if we align all the numbers of a set, and cross off the numbers on each end until we reach the middle, that middle number is the median of the data set.

Mode is the number which appears most commonly in a data set.

Therefore, to find the median and mode of the above set, if would be helpful to arrange the set in numerical order:

The median is the number in the direct middle of the set. In this case, that would be . The mode is the number which appears most often in the set. Since it appears three times,  is the mode of our set. Our final step is to find the mean of these two numbers:

Our final answer is therefore .

The correct answer to this question is 50. In order to approach the problem, you must first start by placing the numbers in order from least to greatest: 27, 34, 44, 56, 67, and 84.

Since there are six numbers in the set, there is not a single number in the middle of the set to be the median.

In this case, we have two numbers in the middle of the set: 44 and 56.

In order to obtain the median, we must take the average of these two numbers.

We do this by completing the following equation: 

To find the median, first put all the numbers in numerical order.

The median is our middle number. Because this set has 6 numbers, our median will fall in between 88 and 92. Average those two numbers to find the median.