All AP Statistics Resources
Example Questions
Example Question #12 : Estimation
You estimate a regression model with 



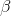
Possible Answers:
Correct answer:
Explanation:
To construct 95% confidence intervals for 



Bhupinder
Certified Tutor
Certified Tutor
Panjab University, Bachelor of Engineering, Biotechnology. Hamburg University of Technology, Master of Science, Chemical Engi...
All AP Statistics Resources
Popular Subjects
Math Tutors in Atlanta, Biology Tutors in San Francisco-Bay Area, Biology Tutors in Houston, ACT Tutors in San Diego, MCAT Tutors in Washington DC, Statistics Tutors in Miami, Calculus Tutors in San Diego, Computer Science Tutors in Miami, MCAT Tutors in Chicago, Physics Tutors in Washington DC
Popular Courses & Classes
MCAT Courses & Classes in New York City, GRE Courses & Classes in New York City, SSAT Courses & Classes in Miami, Spanish Courses & Classes in Chicago, ISEE Courses & Classes in Philadelphia, MCAT Courses & Classes in Atlanta, ISEE Courses & Classes in Houston, ISEE Courses & Classes in Phoenix, SAT Courses & Classes in Atlanta, SSAT Courses & Classes in San Francisco-Bay Area
Popular Test Prep
GRE Test Prep in Dallas Fort Worth, SSAT Test Prep in San Diego, GRE Test Prep in Chicago, GMAT Test Prep in San Francisco-Bay Area, SSAT Test Prep in Boston, SSAT Test Prep in Washington DC, LSAT Test Prep in Atlanta, ISEE Test Prep in Phoenix, SSAT Test Prep in Miami, MCAT Test Prep in Houston

![\left [ 3.1,3.45 \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/37121/gif.latex)
![\left [ 3.4,3.45 \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/37120/gif.latex)
![\left [ 3.35,3.45 \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/37119/gif.latex)



