AP Statistics : Confidence Intervals
Study concepts, example questions & explanations for AP Statistics
All AP Statistics Resources
Example Questions
Example Question #1 : How To Find Confidence Intervals For A Proportion
A health insurance executive suspects that 50% of insurance applications are incomplete (i.e. critical data is missing from the application). He wants to gather a sample to estimate the true proportion. He wants to be within 5% of the true mean with 95% confidence.
What sample size does he need?
385
405
395
365
375
385
Example Question #51 : Inference
You estimate a regression model with 
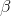
To construct 95% confidence intervals for 
Example Question #61 : Ap Statistics
Which of the following statements are correct about confidence intervals?
The width of a confidence interval does not change as the sample size increases and increases as the confidence level increases.
The width of a confidence interval decreases as the sample size increases and increases as the confidence level increases.
The width of a confidence interval decreases as the sample size increases and increases as the confidence level decreases.
The width of a confidence interval increases as the sample size increases and increases as the confidence level decreases.
The width of a confidence interval increases as the sample size increases and increases as the confidence level increases.
The width of a confidence interval decreases as the sample size increases and increases as the confidence level increases.
Larger samples give narrower intervals. We are able to estimate a population proportion more precisely with a larger sample size.
As the confidence level increases the width of the confidence interval also increases. A larger confidence level increases the chance that the correct value will be found in the confidence interval. This means that the interval is larger.
Example Question #62 : Ap Statistics
You are asked to create a 
Keep in mind that the margin of error for a confidence interval based on a normal population is equal to 
From the problem, we can tell that 
The minimum sample size is 
Example Question #61 : Ap Statistics
Jim calculated a 
More information is needed.
There is a 
In the long run, 
In the long run,
95% confidence means that the methods Jim uses to calculate his confidence interval give him correct results 95% of the time. It does not mean that there is a 95% chance that the true mean will be inside the interval. It also does not mean that 95% of all heights or possible sample means fall within the interval.
Example Question #2 : Confidence Intervals And Regression
The number of hamburgers served by McGregors per day is normally distributed and has a mean of 
First, find the first quartile of the distribution.
Then, find the third quartile of the distribution.
Certified Tutor
All AP Statistics Resources
