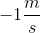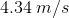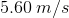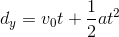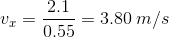All AP Physics C: Mechanics Resources
Example Questions
Example Question #11 : Mechanics Exam
This morning you walked 20 meters to the right from your house to the bus stop, which took you 20 seconds. You waited at the bus stop for 1 minute before realizing you forgot your physics homework at home. You ran back to your house in 5 seconds. It took you 10 seconds to find your homework, and then you ran back to the bus stop in 5 seconds just in time to catch the bus. What was your average velocity for the entire period of motion?
This question tests your understanding of average velocity. You have different velocities throughout your motion: you changed direction and speed several times, including periods of no motion. However, average velocity cares only about your total displacement and how long it took you to get from your initial position to your final position.
Therefore, it is unnecessary to calculate your velocity at each time interval. You know your initial position is at your house and, after the entire motion, your final position is at the bus stop which is 20m to the right of your house. From this we get that the total displacement is 20m (note that it is positive because you moved to the right).
Since you moved back and forth and were motionless for some time intervals, it took you a total of 100s to finally get to the bus stop for good and catch the bus. You need to add all the times for each section of your motion; remember there are 60s in a minute and you need to be consistent with units.
Therefore, your average velocity is:
Example Question #12 : Mechanics Exam
A car undergoes acceleration according to the given function. What distance has the car traveled after three seconds?
We can determine the velocity by taking the second integral of acceleration for the time interval of 0s to 3s.
Solve for the first integral.
Solve for the second integral, using the time interval.
Example Question #11 : Ap Physics C
A car undergoes acceleration according to the given function. How fast is the car moving after four seconds?
We can find the car's velocity by taking the integral of the acceleration function during the given time interval.
Solve the integral for the time interval of 0s to 4s. This will give us the final velocity.
Example Question #11 : Motion
A car undergoes acceleration according to the given function. If the threshold for serious injury or fatality for a human undergoing horizontal acceleration is 60 gees (1 gee = 10 meters per second per second), how long would a human be able to withstand riding in this car?
Calculate the maximum acceration in meters per second.
Solve for the time.
Example Question #11 : Motion
A ball travels with a velocity as described by the function below:
What is the ball's acceleration?
Acceleration is equal to the derivative of the velocity function.
Since the velocity is constant, the derivative will be equal to zero.
The acceleration is equal to zero.
Example Question #1 : Calculating Motion In One Dimension
A man runs with a velocity as described by the function below.
How far does he travel in 1 minute?
Distance is given by the integral of a velocity function. For this question, we will need to integrate over the interval of 0s to 60s.
Example Question #14 : Mechanics Exam
A man runs with a velocity described by the function below.
What is the function for his acceleration?
The function for acceleration is the derivative of the function for velocity.
Example Question #14 : Mechanics Exam
A particle traveling in a straight line accelerates uniformly from rest to 



First off we have to convert 
Next we have to calculate the distance the object traveled the first 5 seconds, when it was starting from rest. We are given time, initial speed to be 

Next, we use the distance equation to find the distance in the first 5 seconds:


If we plug in 

Next we have to find the distance the the object travels at constant speed for 3 seconds. We can use the equation:



Plugging in the equation, we get
Adding 

Example Question #1 : Calculating Motion In Two Dimensions
A 
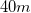
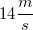

I. Increasing the initial horizontal velocity
II. Decreasing the mass of the ball
III. Throwing the ball from an identical building on the moon
I only
II only
I and III
I, II, and III
I and II
I and III
Relevant equations:

Choice I is true because 




Choice II is false because the motion of a projectile is independent of mass.
Choice III is true because the vertical acceleration on the moon 
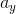


Example Question #1 : Calculating Motion In Two Dimensions
Water emerges horizontally from a hole in a tank 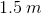
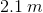
To understand this problem, we have to understand that the water has a x-velocity and a y-veloctiy. The x-velocity never changes.
First we want to find the time it took for the water to hit the ground. We can use this equation:
We know that the y-velocity is 0 to start with, acceleration is 

Substituting into the equation, we get:
Next we have to substitute the time into the equation for the x component
We know that 
Certified Tutor
All AP Physics C: Mechanics Resources