All AP Physics C Electricity Resources
Example Questions
Example Question #1 : Electricity
We have a point charge of 

Coulomb's law for the electric field from point charges is 
Using these values, we can solve for the electric field.
Example Question #4 : Electricity And Magnetism Exam
Two positive point charges of 





To find the location at which the test charge experience zero net force, write the net force equation as 




In this equation, the distance, 




Cross-multiply.
We can cancel 

Now that we have isolated 
Example Question #5 : Electricity And Magnetism Exam
You are standing on top of a very large positively charged metal plate with a surface charge of .
Assuming that the plate is infinitely large and your mass is 
Consider the forces that are acting on you. There is the downward (negative direction) force of gravity, . In order for you to float, there has to be an upward (positive direction) force, and that upward force is coming from the metal plate,
. To show that you would float, the net force equation is written as


For plates that are charged, know that 
Knowing this, the force equation becomes 
Solve for 
Now we can plug in our given values, and solve for the charge.
Example Question #2 : Electricity And Magnetism Exam
A point charge of 


To find the distance between the two charges, use Coulomb's Law.
Since we want to find distance, 

We know the values of the force and the two charges.
We can plug in these values and solve for the distance.
Example Question #3 : Electricity And Magnetism Exam
What is the electric force between two charges, 


The equation for finding the electric force between two charges is 

Now, we can use the values given in the question to solve for the electric force between the two particles.
Example Question #6 : Electricity And Magnetism Exam
What is the magnitude of the electric field at a field point 

The equation to find the strength of an electric field is 
We can use the given values to solve for the strength of the field at a distance of 
Example Question #1 : Using Coulomb's Law
Two capacitors are in parallel, with capacitance values of 

The equivalent capacitance for capacitors in parallel is the sum of the individual capacitance values.
Using the values given in the question, we can find the equivalent capacitance.
Example Question #2 : Using Coulomb's Law
A proton moves in a straight line for a distance of 

The charge of a proton is 
The force of an electric field is given by the equation 


Example Question #13 : Electricity And Magnetism Exam
Two point charges, 



The values of the charges are:
The distance is 4.0cm. The point 

What is the magnitude and direction of the net electric field at point 
At point 


At point P, the electric field due to Q2 points away from Q2 with a magnitude given by
The addition of these two vectors, both pointing in the same direction, results in a net electric field vector of magnitude 152000 volts per meter, pointing toward 
All AP Physics C Electricity Resources





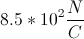
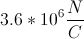












%5E2=kq_2qr%5E2)