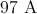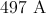Call Now to Set Up Tutoring:

(888) 888-0446

AP Physics C Electricity : Calculating Magnetic Fields and Forces

Study concepts, example questions & explanations for AP Physics C Electricity

Create An Account

All AP Physics C Electricity Resources

1 Diagnostic Test 46 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Calculating Magnetic Fields And Forces

An infinitely long wire has a current of running through it. Calculate the magnetic field at a distance 2cm away from the wire.

$\mu_0=4\pi *10^{-7}\frac{Tm}{A}$

Possible Answers:

$9*10^{-5}T$

$1.5*10^{-3}T$

$3*10^{-5}T$

$2*10^{-4}T$

$7.4*10^{-7}T$

Correct answer:

$3*10^{-5}T$

Explanation:

For infinitely long wires, the formula for the magnetic field is $B=\frac{\mu_0I}{2\pi r}$ , where is the current and is the distance from the wire.

The magnetic field is calculated using our given values.

$B=\frac{(4\pi*10^{-7}\frac{\text{Tm}}{\text{A}})(3\text{A})}{2\pi(0.02\text{m})}$

$B=3*10^{-5}\ \text{T}$

Report an Error

Example Question #41 : Electricity And Magnetism Exam

A solenoid is 50cm long and it is made up of 800 turns of wire. How much current must run through the solenoid to generate a magnetic field of inside of the solenoid?

$\mu_0=4\pi*10^{-7}\frac{Tm}{A}$

Possible Answers:

$583\ \text{A}$

$274\ \text{A}$

$1237\ \text{A}$

$97\ \text{A}$

$497\ \text{A}$

Correct answer:

$497\ \text{A}$

Explanation:

The formula for the magnetic field inside the solenoid is $B=\frac{N}{L}\mu_0I$ , where is the number of turns of wire, is the length of the solenoid, and is the current.

We want to find the current so we solve for .

$I=\frac{BL}{N\mu_0}$

Plug in the values.

$I=\frac{(1\text{T})(0.5\text{m})}{(800)(4\pi*10^{-7}\frac{\text{Tm}}{\text{A}{}})}$

$I=497\ \text{A}$

Report an Error

Example Question #1 : Calculating Magnetic Fields And Forces

Two parallel wires a distance apart each carry a current , and repel each other with a force per unit length. If the current in each wire is doubled to , and the distance between them is halved to $\frac{R}{2}$ , by what factor does the force per unit length change?

Possible Answers:

$\frac{1}{4}$

$\frac{1}{2}$

Correct answer:

Explanation:

Relevant equations:

$\oint B\cdot dl = \mu _o I$

$F = I L \times B$

Step 1: Find the original and new magnetic fields created by wire 1 at wire 2, using Ampere's law with an Amperian loop of radius or $\frac{R}{2}$ , respectively.

Original

$B (2\pi R) = \mu _o I \rightarrow B = \frac{\mu _o I}{2 \pi R}$

New

$B (2\pi (\frac{R}{2})) = \mu _o (2I) \rightarrow B = \frac{\mu _o (2I)}{2\pi \frac{R}{2}} = \frac{4\mu _o I}{2\pi R}$

Since the wires are parallel to each other and wire 1's field is directed circularly around it, in each case wire 1's field is perpendicular to wire 2.

Step 2: Find the original and new magnetic forces per unit length on wire 2, due to the field created by wire 1.

$F = IL \times B \rightarrow \frac{F}{L} = IB$

Original

$\frac{F}{L} = I * \frac{\mu _o I }{2 \pi R} = \frac{\mu _o I^2}{2\pi R}\textup{}$

New

$\frac{F}{L} = 2I * \frac{4\mu _o I}{2\pi R} = \frac{8 \mu _o I^2}{2 \pi R}$

So, the new force per unit length is 8 times greater than the original.

Report an Error

Example Question #1 : Calculating Magnetic Fields And Forces

A region of uniform magnetic field, , is represented by the grey area of the box in the diagram. The magnetic field is oriented into the page.

Ps0_movingqinbfield

A stream of protons moving at velocity $\vec{v}$ is directed into the region of the magnetic field, as shown. Identify the correct path of the stream of protons after they enter the region of magnetic field.

Possible Answers:

A semi-circular path oriented vertically downward

A semi-circular path oriented horizontally out of the page

A semi-circular path oriented horizontally into the page

A semi-circular path oriented vertically upward

Correct answer:

A semi-circular path oriented vertically upward

Explanation:

The magnetic force on a moving charged particle is given by the equation:

$\vec{F}=q\,\vec{v}\times \vec{B}$

Isolating the directional component of this equation yields the understanding that the resulting force on a moving charged particle is perpendicular to the plane of the velocity vector and magnetic field vector. Using the right-hand-rule on this cross-product shows that the velocity vector right-crossed into the magnetic field vector into the page yields a magnetic force vector upward on a positive charge. This will result in a semi-circular path oriented vertically upward.

Report an Error

View Tutors

Aidan
Certified Tutor

Case Western Reserve University, Electrical Engineer, Electrical Engineering.

View Tutors

Dossevi
Certified Tutor

cole Ste Genevive Versailles, Bachelor of Science, Mathematics. Institut National Polytechnique de Grenoble, Master of Scienc...

View Tutors

Gregory
Certified Tutor

Pennsylvania State University-Main Campus, Bachelor of Science, Chemical Engineering. Carnegie Mellon University, Doctor of P...

All AP Physics C Electricity Resources

1 Diagnostic Test 46 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Reading Tutors in Dallas Fort Worth, SSAT Tutors in Philadelphia, MCAT Tutors in Los Angeles, GRE Tutors in Philadelphia, English Tutors in Denver, ISEE Tutors in Phoenix, Statistics Tutors in Miami, Biology Tutors in Denver, ACT Tutors in Philadelphia, ISEE Tutors in Dallas Fort Worth

Popular Courses & Classes

ISEE Courses & Classes in Boston, ACT Courses & Classes in Phoenix, ISEE Courses & Classes in Philadelphia, SSAT Courses & Classes in Phoenix, ACT Courses & Classes in New York City, Spanish Courses & Classes in Atlanta, ACT Courses & Classes in Seattle, GMAT Courses & Classes in Boston, ISEE Courses & Classes in Seattle, SAT Courses & Classes in Denver

Popular Test Prep

LSAT Test Prep in Atlanta, SAT Test Prep in Los Angeles, ACT Test Prep in Seattle, SSAT Test Prep in Houston, LSAT Test Prep in Seattle, GMAT Test Prep in Boston, SAT Test Prep in Seattle, LSAT Test Prep in Miami, SAT Test Prep in Chicago, SSAT Test Prep in Los Angeles

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

AP Physics C Electricity : Calculating Magnetic Fields and Forces

Study concepts, example questions & explanations for AP Physics C Electricity

All AP Physics C Electricity Resources

Example Questions

Example Question #1 : Calculating Magnetic Fields And Forces

Example Question #41 : Electricity And Magnetism Exam

Example Question #1 : Calculating Magnetic Fields And Forces

Example Question #1 : Calculating Magnetic Fields And Forces

All AP Physics C Electricity Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: