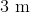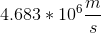AP Physics 2 : Quantum and Nuclear Physics
Study concepts, example questions & explanations for AP Physics 2
All AP Physics 2 Resources
Example Questions
Example Question #1 : Principles Of General Relativity
A student on the Earth observes a spaceship moving at a considerable fraction of the speed of light. As a result of the spaceship's motion, the student observes that the clocks aboard the spaceship are running slower than when the spaceship was on the Earth. When a student aboard the spaceship observes the student's clock on the Earth, what effect will he notice on the rate of the Earth-bound clock?
The Earth-bound clock appears to run slower
The Earth-bound clock runs at the same rate
The Earth-bound clock appears to run faster
The Earth-bound clock first runs slow, then fast
The Earth-bound clock first runs fast, then slow
The Earth-bound clock appears to run slower
For the observer on the spaceship, the Earth appears to be moving, and special relativity tells us that any observer moving at constant speed can consider him/herself stopped. Therefore, the clock on the Earth experiences the same slowing from the spaceship's viewpoint as the spaceship's clock from the Earth viewpoint. It's a little bit like looking at someone from far away. They look small due to the distance, but you do not look big to them, you also look smaller.
Example Question #1 : Principles Of Special Relativity
Determine the observed length of a 
Using the formula for length contraction:
Where 
Plugging in values
Example Question #1 : Principles Of Special Relativity
Determine the observed length of a 
None of these
Use the following equation:
Where
Plugging in values
Example Question #1 : Principles Of Special Relativity
A 
None of these
Using
Plugging in values
Example Question #3 : Principles Of Special Relativity
A 
None of these
Using
Plugging in values
Example Question #1 : Other Principles Of Quantum Mechanics
A proton is confined to a one-dimensional box of length 
Fourth excited state.
Not enough information to solve the problem.
Ground state.
Second excited state.
Second excited state.
The energy of the quantum system in the 
where 
where 
Since the ground state is 
Example Question #1 : Other Principles Of Quantum Mechanics
The expectation value 
The energy of the particle
The exact location of the particle
If the particle exists or not
The momentum of the particle
The most probable location of the particle
The most probable location of the particle
From a statistical standpoint, the expectation value of the position, 
Example Question #2 : Other Principles Of Quantum Mechanics
If a particle in a quantum system is bounded, this means what about the calculated particle energy?
The energy must be negative and continuous.
The energy must be positive and continuous.
The energy is described by discrete energy levels, and the particle can only have energy that corresponds to these levels, positive or negative.
There is nothing constraining the energy of the particle.
The energy of the particle can be anything, positive or negative.
The energy is described by discrete energy levels, and the particle can only have energy that corresponds to these levels, positive or negative.
A key characteristic of bound-state systems is the quantization of the energy into discrete energy levels. The energy can be negative or positive, but the particle can only have an energy that corresponds to one of these energy levels, nothing other. An example is the energy of a hydrogen atom, where the energy levels are given by:
These discrete numbers come from the energy of an electron, which is the fundamental charge.
Example Question #4 : Other Principles Of Quantum Mechanics
The square modulus of the wavefunction, given as 
By definition, 
Example Question #1 : Atomic And Nuclear Physics
What is the speed of an electron in the first Bohr orbit in meters per second?
To find the speed of the electron, use the following formula:
Substitute all the knowns and solve for velocity.
All AP Physics 2 Resources
