All AP Physics 2 Resources
Example Questions
Example Question #21 : Quantum And Nuclear Physics
Which of the following subatomic particles has the highest charge to mass ratio?
Neutron
Gluon
Antiproton
Electron
Proton
Electron
Neutrons and gluons both have no charge at all, so they can be ignored. The proton and the antiproton have the same mass but opposite charges, and so have the same ration of charge:mass. However, the electron has equal charge to both the proton and the antiproton, and has a ridiculously small mass comparatively. The mass of a proton/antiproton is 
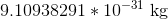
Example Question #11 : Atomic And Nuclear Physics
Compound X is found to radioactively decay with a rate constant equal to 
To begin with, we'll have to make use of the radioactive decay equation:
Where:





Rearranging, we can see that:
Furthermore, we can convert minutes into seconds.
Next, we can plug the values we have into the above equation to obtain:
From the above expression, we see that:
This means that after a time of 20min has elapsed, there will be 


Example Question #361 : Ap Physics 2
Which of the following types of decay particles is known as a positron?




None of these particles are known as positrons

Positron decay (positive beta decay) is where a proton is converted into a neutron, a positron, and an electron neutrino.
Positrons are called 

Example Question #11 : Atomic And Nuclear Physics
The half-life of carbon-14 is 5730 years.
Rex the dog died in 1750. What percentage of his original carbon-14 remained in 1975 when he was found by scientists?
225 years have passed since Rex died. Find the number of half-lives that have elapsed.
To find the proportion of a substance that remains after a certain number of half-lives, use the following equation:
Here, 
Example Question #12 : Atomic And Nuclear Physics
You measure the beta decay activity of an unknown substance to be 

What is the half life in hours?
Use the following equation:
The decay constant is defined as:
From the first equation, we find:
Plug this value into the second equation above and solve.
Example Question #2 : Radioactive Nuclear Decay
A particular sample of a newly discovered isotope has an activity of 

Determine the radioactive decay constant of this isotope.
None of these
Use the relationship:
Here, 



Rearrange the equation to solve for 
Convert minutes to seconds and plug in values to solve for the radioactive decay constant.
Example Question #3 : Radioactive Nuclear Decay
A scientist tests a radioactive sample which has an activity of 

Determine the number of radioactive nuclei in the initial sample.
None of these
Use the relationship:
Where 



Rearrange to solve for 
Convert minutes to seconds and plug in values to find the decay constant.
It is then necessary to use the relationship:
Where 


Use the initial activity and the calculated decay constant to solve for the number of atoms:
Example Question #2 : Radioactive Nuclear Decay
A scientist tests a radioactive sample which has an activity of 

Determine the activity 18 minutes after the initial reading.
None of these
Use the relationship:
Where 



Rearrange to solve for
Convert minutes to seconds and plug in values.
Again use the relationship:
Use the new 

Example Question #1 : Radioactive Nuclear Decay
A scientist test a radioactive sample which has an activity of 

Determine the half life of this isotope.
None of these
Use the relationship:
Here, 



Rearrange the equation to solve for 
Convert minutes to seconds and plug in values.
Use the relationship:
Plug in the calculated value for 
Example Question #4 : Radioactive Nuclear Decay
A scientist test a radioactive sample which has an activity of 

Determine the nuclear decay constant of this isotope.
None of these
Use the relationship:
Here, 



Rearrange the equation to solve for 
Convert minutes to seconds and plug in values.
Certified Tutor
Certified Tutor
All AP Physics 2 Resources




































































