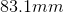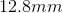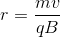All AP Physics 2 Resources
Example Questions
Example Question #1 : Magnetic Force
A particle with a charge of 


There is no force on the particle
The equation for finding the force on a moving charged particle in a magnetic field is as follows:
Here, 




Another way to write the equation without the cross-product is as follows:
Here, 
For our problem, because theta is 

Therefore, the force on the particle is 0.3N.
Example Question #2 : Magnetic Force
An 



The wire doesn't experience any force
The equation for the force on a current carrying wire in a magnetic field is as follows:




Because our wire is not fully perpendicular to the magnetic field, it does not experience the full possible force. Instead, it experiences 
Example Question #2 : Magnetic Force
A proton traveling at 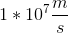


The proton’s mass is 


A charged particle moving through a perpendicular magnetic field feels a Lorentz force equal to the formula:



We can set these two equations equal to one another, allowing us to solve for the radius of the arc.
Once the particle travels through a semicircle, it is laterally one diameter in distance from where is started (i.e. twice the radius of the circle).
Twice this value is the lateral offset of its crash point from the entrance:
Example Question #3 : Magnetic Force
What is the force experienced by a 



There is no net force on the charge
To find the force experienced by the charge, we use this equation:
Because the charge is moving at an angle from perpendicular, we need to take the cross product into account.
Theta is the angle from perpendicular, which is 
Example Question #3 : Magnetic Force
An 


There is no force on the charge
The equation for force on a charge moving through a magnetic field is:
Because the velocity is perpendicular to the field, the cross product doesn't matter, and we can do simple multiplication.
Therefore, the force on the charge is
Example Question #5 : Magnetic Force
A 



The charge experiences no force
The equation for force on a charge moving through a magnetic field is:

The cross product is:
Above, 

The force on the charge is about 
Example Question #1 : Magnetic Force
A particle is moving parallel to a uniform magnetic field. Which of the following statements are true?
The particle experiences the most force possible in the setup
The magnetic field is exerting no force on the particle
None of the other statements are certain
The particle will rotate around a point in the magnetic field
The particle has no net charge
The magnetic field is exerting no force on the particle
The force experienced by a charged particle in a magnetic field is
This means that when a charge particle is moving perpendicular to the field, due to the cross-product, it experiences the most amount of force (because 


Example Question #1 : Magnetic Force

A rail system is formed in a magnetic field directed out of the page as diagrammed above. The rod remains in contact with the rails with zero friction as it moves to the right at a constant velocity of 

No force is necessary since the rod is moving at a constant velocity




The rod acts as a battery due to its motion in the magnetic field: 
In this simple circuit, the current is the same everywhere, so the same current flows through the rod. Because of this current, the rod feels a force:
By the right-hand rule, this magnetic force is directed to the left, so the external force must be directed to the right. It is interesting to note that the power dissipated in the resistor:

The universe conspires to conserve energy.
Example Question #23 : Magnetism And Electromagnetism
If a 10C charged particle is traveling perpendicularly to a magnetic field of 5T at a speed of 
This question is presenting us with a scenario in which a charged particle is traveling with a certain velocity through a magnetic field. In this situation, we're being asked to determine what the force experienced by this particle is.
To solve this question, we'll need to determine what kind of force this particle is likely to experience. Since we're told that the particle is traveling in a magnetic field, it would make sense that this particle is going to be affected by a magnetic force. Thus, we'll need to use the equation for magnetic force.
Moreover, since we're told in the question stem that this particle is traveling perpendicularly to the magnetic field, we know that 

Now, all we need to do is plug in the values given to us in order to calculate the resulting force.
Example Question #671 : Ap Physics 2
A charged particle, Q, is traveling along a magnetic field, B, with speed v. What is the magnitude of the force the particle experiences?
Zero
Zero
Charged particles only experience a magnetic force when some component of their velocity is perpendicular to the magnetic field. Here, the velocity is parallel to the magnetic field so the particle does not experience a force.
All AP Physics 2 Resources