All AP Physics 1 Resources
Example Questions
Example Question #252 : Forces
2 objects(named object A and object B) of equal masses and initial kinetic energy collide onto one another. During the collision, object A loses 
Given that object A's mass is 


Force is given by:



We're given mass, but we aren't given acceleration. Since the question asks for average force 




In our problem, 
Example Question #13 : Newton's Second Law
A block with a mass of 


Here we must use the following formula:
We can substitute our known values of mass and force and solve for acceleration
Since we know the acceleration and the time it acts upon the object, we can determine the final velocity through the following equation:
Example Question #253 : Forces
Consider a block sitting at rest on an inclined plane. Find the maximum inclination angle the plane may have without the block sliding if the coefficients of kinetic and static friction are 
If the block is to remain at rest on the plane, we know that the sum of the forces acting a long the plane must be equal and opposite. This means that the gravitational force acting along the plane is equal to and opposite of the force of friction. This can be demonstrated as:
This can be rewritten as:
For the block to remain at rest, the force of static friction must exceed (for this problem we will set them equal to each other since it gives us the best approximation); solve for the angle:
Example Question #15 : Newton's Second Law
A force of 

What is the acceleration of the object?
Newton's second law states:
Where 


We rearrange this equation to show:
Plug in our given values with 

Example Question #861 : Ap Physics 1
If 



By Newton's second law:





This is the acceleration. Since we're assuming this acceleration is constant over time, we can model velocity 


Since the initial velocity is 

After 
Example Question #17 : Newton's Second Law
A train of mass 




Use work:
All energy will be kinetic.
Convert 

Plug in values. Force will be negative as it is pointing against the direction of travel:
Solve for 
Use Newton's second law:
Plug in values:
Solve for 
Convert to
Example Question #252 : Forces
A train of mass 



Use work:
All energy will be kinetic.
Convert 

Plug in values. Force will be negative as it is pointing against the direction of travel:
Solve for 
Use frictional force:
Plug in values:
Solve for
Example Question #31 : Fundamentals Of Force And Newton's Laws
Suppose that an astronaut on the moon applies a horizontal force of 


In this question, we're told that a horizontal force is being applied to an object on the moon. We're given the magnitude of this force and the mass of the object.
We're also given the acceleration due to gravity on the moon, but this is useless information for the purposes of this question. Since the force under consideration is acting horizontally on the object, and the force due to gravity acts vertically, these two forces are treated separately; the vertical acting force of gravity will not affect the horizontal kinematics of the object's movement.
Thus, this reduces to a simple application of Newton's second law, and we can use the following equation:
Rearranging, we can isolate the term for acceleration:
Then plug in the values that we have to solve for our answer:
Example Question #32 : Fundamentals Of Force And Newton's Laws
Consider the following system:

Two spherical masses, A and B, are attached to the end of a rigid rod with length l. The rod is attached to a fixed point, p, which is at a height, h, above the ground. The rod spins around the fixed point in a vertical circle that is traced in grey. 

The rod is initially at rest and held in the horizontal position. When it is released, what is the initial instantaneous acceleration of mass A, and in what direction? Assume the rod has a negligible mass. Neglect air resistance and internal frictional forces.
None of the other answers
This problem can be solved using the expression relating torque and angular acceleration:
We can determine the total net torque on the system using the Newton's second law.
Applying this to both masses and assuming a force in the downward direction is positive, we get:
Then using the expression for torque, we get:
Where d is half the length of the rod.
Applying this to both masses and assuming torque in the counterclockwise direction is positive, we get:
Now let's go back to the original equation:
Now we need to calculate the net moment of inertia:
Where r is half the length of the rod:
Going back to the original equation and rearranging for angular acceleration:
Then relating this to linear acceleration using:
Where r is half the length of the rod again:
We have all of our values, so we can calculate the final answer:
Example Question #41 : Fundamentals Of Force And Newton's Laws
Consider the following system:
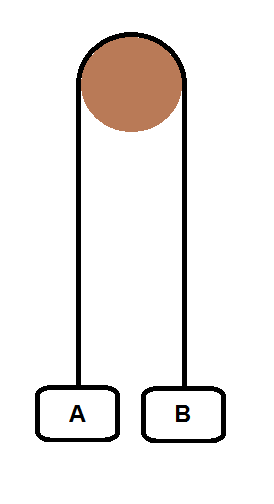
Two masses, A and B, are attached to the end of a rope that runs through a frictionless pulley.
The two masses are initially held at rest. When they are released, what is the initial instantaneous acceleration of mass A, and in what direction? Neglect air resistance and any frictional forces.

We can use Newton's second law:
There are two forces acting on the system: gravity on each mass. For simplicity sake, we will examine these forces with respect to mass. Therefore, the force on mass B becomes an upward tension force on mass A. Now we need to clarify which direction is positive. For this problem, we'll say that a downward force is positive, and an upward force is negative.
We'll start with the gravitational force:
Now for tension. The tension force is simply the gravitational force applied to mass B:
Note that it's negative because it is in the upward direction
Now adding these together to get the net force:
Substituting this back into the original equation, we get:
Where m is the combination of both masses:
Rearrange for acceleration:
We know each value, so we can solve the problem
Certified Tutor
Certified Tutor
All AP Physics 1 Resources






















































































































