All AP Physics 1 Resources
Example Questions
Example Question #81 : Motion In Two Dimensions
A home run derby is being held in a stadium where the home run wall is 


Neglect air resistance and assume
If a baseball pitcher standing at home plate is able to throw a ball at 

No, he misses the top of the wall by
Yes, he clears the top of the wall by
It is impossible to determine from the given information.
No, he misses the top of the wall by
Yes, he clears the top of the wall by
No, he misses the top of the wall by
There are multiple ways to determine if the pitcher can throw the ball over the wall or not. The following method will determine what the maximum height of the ball will be when it reaches the wall. In other words, what will the height of the ball be when it reaches the wall if thrown at an angle of 
So the values we will use are:
Let's begin with the following kinematic equation:
Where:
Plugging in expressions for our component velocities, we get:
Since our angle is 45, sin = cos. Let's simplify things and make everything sin:
Substituting this into the kinematic expression, we get:
Plugging in our values, we get:
He is so close!
Example Question #90 : Motion In Two Dimensions
A home run derby is being held in a stadium where the home run wall is 


Neglect air resistance and assume
A batter hits a home run with a total distance of 


We can use the following piecewise function to determine the height of the ball as a function of the horizontal distance it has traveled:
If 
If 
We can calculate the final height of the ball with the given horizontal distance:
Then we can use the following kinematic expression:
Plugging in our values:
The shorter time is the first instance that the ball passes through a height of 20 meters, and the second time is when the ball lands in the stands. Thus,
If you are wondering why the two times are relatively close, do some math and check out the maximum height of an object that has an initial vertical velocity of
Example Question #91 : Motion In Two Dimensions
Find the vector going from point A to point B, shown on the graph below.
The correct answer is 
Example Question #451 : Ap Physics 1
A remote control car slides off a curb .2 meters high and lands 1 meter from the base of the curb. Select the initial horizontal velocity of the car.
To solve this problem you must consider (separately) the x and y components of an object that is both moving horizontally and vertically.
For the vertical component we find the time that the car was in the air:
Keep in mind the acceleration vertically is just gravity.
*Make gravity negative because it pulls downward and the height negative because the object is falling. You could also just remember that time can't be negative and ignore the signs.
Solve for t:
For the horizontal component we use:
Acceleration in the horizontal is 0.
Example Question #93 : Motion In Two Dimensions
Object X has initial velocity 



None of these
Definition of momentum:
Combine equations:
Plug in values:
Example Question #1 : Impulse And Momentum
In a billiards game, one player hits the cue ball towards another ball. The cue ball has a mass of 0.1kg and hits the other ball with a velocity of 

Since the collision is completely elastic, we know that both momentum and kinetic energy are conserved. We can write the following equations (initial momentum and energy of the second ball are neglected since it is not moving:
Rearrange the first equation for 

We can rewrite the second equation as:
Substitute our equation for 
Rearranging, we get:
Plug in our values for the initial and final velocities:
To solve for mass, we'll use our earlier expression for 
Example Question #2 : Impulse And Momentum
Two sumo wrestlers are in a match. At the start of the match, they both lunge at each other. They hit and miraculously come to a stand still. One wrestler was 200kg and traveling at a velocity of 

It does not matter whether the collision is elastic or inelastic (although it would be best to assume that it's inelastic). Momentum is conserved in either type of collision, and is the only value needed for our calculation. Since they come to a standstill, their momentums at the moment of collision are equal and opposite:
Rearrange to solve for 
Plug in the given values from the question and solve:
Example Question #1 : Impulse And Momentum
One car with a mass of 400kg is traveling east at 

Since the collision is completely inelastic, momentum is conserved but energy is not. Furthermore, the two cars stick to each other and travel as one. The equation for conservation of momentum is as follows:
There are two inital masses with different velocities and one final mass with a single velocity. Therefore, we can write:
Rearranging for final velocity, we get:
At this point, we can denote which direction is positive and which is negative. Since the car traveling west has more momentum, we will consider west to be positive. Substituting our values into the equation, we get:
Since this value is positive, the final answer is 
Example Question #461 : Ap Physics 1
A marble of mass 

Impulse can be written as either of two popular expressions:
From the problem statement, we can determine the velocity of the marble as it hits the floor, allowing us to use the latter expression. To determining the velocity of the marble, we can use the equation for conservation of energy:
Assuming the final height is zero, we can eliminate initial kinetic energy and final potential energy. Therefore, we can write:
Canceling out mass and rearranging for final velocity, we get:
We know these variables, allowing us to solve for the velocity:
Plugging this value into the expression for impulse, we get:
Example Question #1 : Impulse And Momentum
Consider the following system:
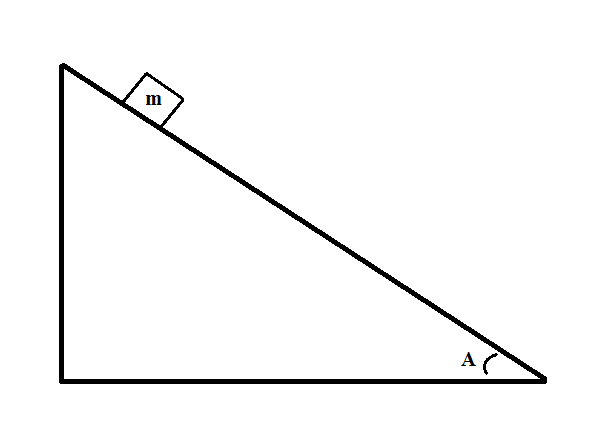
If the block has a mass of 


To calculate the momentum of the block, we first need to know the velocity of the block. This can be found using the equation for the conservation of momentum:
If we assume that the final height is zero, we can eliminate initial kinetic energy and final potential energy, getting:
Substituting expressions for each term, we get:
Cancel out mass and rearrange to solve for velocity:
We can use the horizontal distance traveled and the angle of the slope to determine the initial height:
Now that we have the initial height, we can solve for final velocity:
Finally, we can now use the equation for momentum to solve the problem:
Certified Tutor
All AP Physics 1 Resources




































































































































