All AP Physics 1 Resources
Example Questions
Example Question #1 : Gravitational Potential Energy
A lazy contractor of mass 80kg who is bricking a building figured out that a seesaw makes his life much easier. He needs to deliver bricks to his coworker who is 10 meters above him. The contractor puts bricks on one side of the seesaw and jumps on the other side to fling the bricks upward. If the contractor jumps onto the seesaw from a height of 1.5 meters, what is the maximum mass of bricks he can put on the seesaw that will reach his coworker?
This problem can either be very simple or very complex.
You could convert the contractor's potential energy into kinetic energy, and then find the velocity at which he hits the seesaw. Then, use that to calculate the kinetic energy of the bricks and the height at which the bricks will fly. Although some may find that fun to do, it's unnecessary.
If we assume that all of the energy of the man is transferred to the bricks, we can use the conservation of energy equation:
We need to make a few clarifying statements for our initial and final states. In the initial state, the contractor is at a height of 1.5m and not moving. The bricks are not moving at this point either. In the final state, the man is on the ground not moving, and the bricks are at a height of 10m and not moving. Therefore, we can rewrite the above equation as the following:
Rearranging for the mass of the bricks:
Example Question #1 : Gravitational Potential Energy
A basketball player goes for a 3-point shot, but misses. The basketball has a mass of 


Using the equation for conservation of energy, we get:
Let's clarify that our initital state is when the ball is at its maximum height and the final state is when it reaches the ground. Plugging in our expressions and removing initial kinetic and final potential energy, we get:
Note that we removed initial kinetic energy despite the ball moving. At the initial state, all of the ball's velocity is horizontal. Since there is no vertical velocity, we can ignore it for now, coming back to it later.
We multiply the initial energy by 0.85 because the problem statement says that we lose 15% of the ball's total energy after hitting the rim. Rearranging for final velocity:
This is only the y-component of the final velocity. We need to combine this with the x-component to get the total velocity. The problem statement tells us that the final horizontal velocity is 
Example Question #1 : Gravitational Potential Energy
Consider the following system:
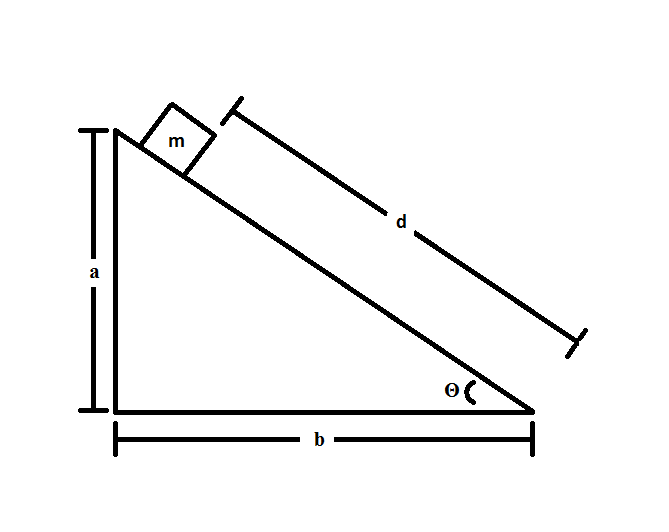
If 


This problem helps you become more comfortable with using obscure units. Since we are given work as a function of mass, we don't actually have to know the mass of the block. Furthermore, since we are neglecting air resistance, we know that all of the work is done by friction. To calculate the force of friction, we can use the following expression:
To calculate the work done by this force, we multiply by the distance that it was applied:
Since we were given work as a function of mass, we can eliminate mass to get:
Rearranging for the angle, we get:
We know all of these values, allowing us to solve for the angle:
Example Question #1 : Gravitational Potential Energy
A mountain biker goes off a jump with an initial vertical velocity of 

We can use the expression for conservation of energy to solve this problem:
Assuming a final height of zero, we can eliminate final potential energy. Then, substituting in expressions for each variable, we get:
Canceling out mass and rearranging for final velocity, we get:
Example Question #1 : Gravitational Potential Energy
A rock is lifted 10m off of the ground, carried by the person holding it across a field of length 100m, and held at a final height of 10m. What was the change in gravitational potential energy?
The change in gravitational potential energy is only dependent on the final and initial height of the object, and is independent of the path taken to get to the final height. Because the change in height for the rock is zero, the change in gravitational potential energy equals zero.
Example Question #1 : Gravitational Potential Energy
A dumbell with a mass of 

Over the distance described, change in gravitational pull is negligible, so gravity can be treated as a constant. Potential energy therefore varies with the dumbell's proximity to the ground, h:
Since the dumbell has an inital position of 100m, and an initial velocity of zero, its height can be described using the kinematic equation:
From this, the potential energy at a time of three seconds is:
Example Question #6 : Gravitational Potential Energy
A 

The first step for this problem is to determine the potential energy the ball has at the top of the ramp through this equation:
We see that it has a potential energy of 100 joules. All of this potential energy gets converted to kinetic energy as the ball falls down the ramp.
Knowing this, we can determine the velocity the ball has at the bottom of the ramp by setting the potential energy equal to the kinetic energy:
We substitute the known mass and solve for 
Example Question #7 : Gravitational Potential Energy
A ball with a mass of 2kg hangs from a cord 1.4 meters in length from the ceiling of a room with a total height of 3.1 meters. What is the gravitational potential energy of the ball relative to the ceiling? Assume the acceleration of gravity 
None of these
Gravitational potential energy is proportional to both the height and mass of an object. Gravitational potential energy is given by:

Gravitational potential energy is also relative to a "zero height" and in our case this is the ground. What this means is that if the ground is a our "zero height", the higher the object from the ground the greater the potential energy
Example Question #1 : Gravitational Potential Energy
Two balls of equal mass (3kg) are hanging from cords 1.5 meters and 2 meters in length from a ceiling in a room with a total height of 3 meters. Which has a greater gravitational potential energy relative to the floor? Assume the acceleration of gravity is 
The ball with the shorter cord
They have the same gravitational potential energy since they have the same mass
There is a negligible difference
The ball with the longer cord
Cannot be determined without knowing the density of the masses
The ball with the shorter cord
Gravitational potential energy is proportional to both the height from a "zero potential energy" reference point (in our case the floor) and the mass. While the balls would have the same gravitational potential energy since they are the same mass, they have differing energies because of differing heights. The shortest cord, or the ball the highest from the ground will have the greatest potential energy as shown:
Example Question #1 : Gravitational Potential Energy
A cart is traveling at 

How high will the ball go?
None of these
Use conservation of energy:
Plug in known values and solve for the maximum height of the object.
All AP Physics 1 Resources




























































































