All AP Physics 1 Resources
Example Questions
Example Question #81 : Fundamentals Of Force And Newton's Laws
Consider the following system:
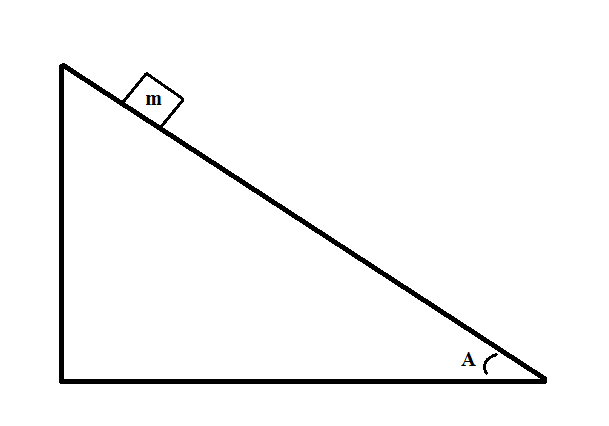
If the mass accelerates down the plane at a rate of 

Before we start using equations, we need to determine what forces are acting on the block in this system. The only relevant forces in this situation are gravity and friction. We are given the acceleration of the block, giving us the tools to find the net force.
Using Newton's second law, we can write:
The force of friction is subtracted because it is in the opposite direction of the movement of the block. Substituting in expressions for each variable, we get:
Canceling out mass and rearranging for the coefficient of kinetic friction, we get:
We have values for each variable, allowing us to solve:
Example Question #82 : Fundamentals Of Force And Newton's Laws
Consider the following system:

This system is set on a different planet, which has a gravitational constant different from that on Earth. If the angle measures 


There are two relevant forces acting on the block in this scenario: gravity and friction. We can use Newton's second law to solve this problem:
Substituting in expressions for each force, we get:
Eliminating mass and rearranging for 
At this point, we can plug in values for each variable and solve:
Example Question #1 : Force Diagrams

In the diagram, a massless string connects two blocks of mass 30 kg and 50 kg that are on a flat, frictionaless surface. A force 

Start by drawing in the forces acting on each block. You could also draw in the force of gravity and the normal force for each block, but they have been omitted from the image because they cancel each other out for each block and because there is no friction in this problem.

We are given in the question that the force 
In this problem, the two tension forces form an action/reaction pair and therefore are equal in magnitude but opposite in direction (Newton's third law). So:
We can solve for acceleration, since the tensions cancel out.
Now that we have acceleration, we need to write a new equation in which the tension force does not cancel out so that we can solve for the tension 
Do this by using Newton's second law again, except for only one of the blocks:
Lets consider the 30 kg block. The only force acting on the 30 kg block is the tension 
Example Question #2 : Force Diagrams
A ball with mass 

Find the magnitude of the ball's normal force.
The normal force is perpendicular to the plane:

First, we need to find 
We can solve for 



Rearranging to solve this equation for 
Substituting in the side lengths of the given triangle, we can solve for 
Note that the normal force is one of the legs of another right triangle. The other leg is the parallel force, and the hypotenuse is the force of gravity.
Using trigonometry, we know that
because 

Substituting in the known values into this equation, we can solve for the normal force:
Example Question #5 : Force Diagrams

What is the acceleration of the block above if its mass is 

Not enough information given

The component of 




The force of friction, which is in the direction opposing motion is:

The component of 
The net force on the block is:

Example Question #921 : Ap Physics 1

A mass is suspended by two cables. What is the magnitude of the tension in the left cable?
Begin by diagraming the forces acting on the mass in the problem:

The mass itself creates a force due to gravity in the downward direction:
For the mass to remain stationary, the forces must be in equilibrium. Therefore the sum of forces in the x and y directions each must be zero:
The x and y tensions can be written in terms of the magnitude of the tension in each cable. Begin with the x direction:
Because the angle is the same for each, the tension in each angle must be equivalent. Use this property when performing the force balance in the y direction:
Example Question #7 : Force Diagrams

A mass is supported by two cables. What is the magnitude of tension in the right cable?
Begin by drawing a force diagram of forces acting on the mass:

The mass itself creates a force due to gravity in the downward direction.
For the mass to remain stationary, the forces must be in equilibrium. Therefore the sum of forces in the x and y directions each must be zero:
The x and y tensions can be written in terms of the magnitude of the tension in each cable. Begin with the x direction:
Because the angle is the same for each, the tension in each angle must be equivalent. Use this property when performing the force balance in the y direction:

Example Question #91 : Fundamentals Of Force And Newton's Laws

A 50kg mass is supported by two cables. Find the magnitude of tension in the left cable.
Begin by diagraming the forces acting on the mass:

The mass itself creates a force due to gravity in the downward direction.
For the mass to remain stationary, the forces must be in equilibrium. Therefore the sum of forces in the x and y directions each must be zero:
The x and y tensions can be written in terms of the magnitude of the tension in each cable. Begin with the x direction:
Because the angle is the same for each, the tension in each angle must be equivalent. Use this property when performing the force balance in the y direction:

Example Question #1 : Force Diagrams
Which of the following is true when an object has reached terminal velocity?
During terminal velocity:
Thus, by Newton's second law:
Example Question #10 : Force Diagrams
A block of mass 




What is the value of 





The free body diagram of the block is given above. This block has three forces acting on it. First, it's weight under the influence of gravity, which is given as 






Now we can use Newton's 2nd law to relate the given forces above. Newton's 2nd law gives us two equations:

Because the block is constrained to move along the surface of the inclined plane, there should be no acceleration in the y direction, and so 


Summing all the forces in the x-direction gives us

Summing all the forces in the y-direction gives us

Plugging these values into the force equations above gives us the following equations:
Solving for 



Now we solve the equation for 

Now we divide each side by 
The final result is obtained by canceling the 
Therefore we arrive at the conclusion that
All AP Physics 1 Resources
























































































































