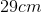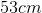AP Physics 1 : Circular, Rotational, and Harmonic Motion
Study concepts, example questions & explanations for AP Physics 1
All AP Physics 1 Resources
Example Questions
Example Question #1 : Torque
Two students are balancing on a 10m seesaw. The seesaw is designed so that each side of the seesaw is 5m long. The student on the left weighs 60kg and is standing three meters away from the center. The student on the right weighs 45kg. The seesaw is parallel to the ground. Assume the board that makes the seesaw is massless.
Imagine that the two students are sitting on the seesaw so that the torque is 
The heavier student moves forward 1m, while the lighter student moves forward 1.33m.
Both students move toward the center by one meter.
Two more students get on the seesaw, each weighing 45kg. They both sit on opposite ends of the seesaw, five meters away from the center.
Another student stands perfectly on the center of the seesaw.
Both students move toward the center by one meter.
Torque, in this case, is dependent on both the force exerted by the students as well as their distances from the point of rotation. As a result, both students moving forward by one meter will cause a nonzero torque on the seesaw. This is because the heavier student's ratio of force and distance will result in less torque on his side than the lighter student.
Example Question #1 : Torque
A 3m beam of negligible weight is balancing in equilibrium with a fulcrum placed 1m from it's left end. If a force of 50N is applied on it's right end, how much force would needs to be applied to the left end?
This a an example of rotational equilibrium involving torque. The formula for torque is 
Since the forces are applied perpendicular to the beam, 
Since the 50N force is twice as far from the fulcrum as the force that must be applied on the left side, it must be half as strong as the force on the left. The force on the left can be found to be 100N.
Example Question #1 : Torque
One side of a seesaw carries a 
For the seesaw to be balanced, the system must be in rotational equilibrium. For this to occur, the torque the same on both sides.
The total torque must be equal on both sides in order for the net torque to be zero.
Substitute the formula for torque into this equation.
Now we can use the given values to solve for the missing mass.
The acceleration form gravity cancels from each term.
Example Question #1 : Torque
Two masses hang below a massless meter stick. Mass 1 is located at the 10cm mark with a weight of 15kg, while mass 2 is located at the 60cm mark with a weight of 30kg. At what point in between the two masses must the string be attached in order to balance the system?
This problem deals with torque and equilibrium. Noting that the string is between the two masses we can use the torque equation of 
x=43, thus the string is placed at the 43cm mark.
Example Question #1 : Torque
An attraction at a science museum helps teach students about the power of torque. There is a long metal beam that has one pivot point. At one end of the bar hangs a full sedan, and on the other end is a rope at which students can pull down, raising the car off the ground.
The beam is 40 meters long and the pivot point is 5 meters from one end. A car of mass 500kg hangs from the short end of the beam. Neglecting the mass of the beam, what is the minimum mass of a student who can hang from the rope and begin to raise the car off the ground?
More information is needed to answer
We are trying to find what force needs to be applied to the rope to result in a net of zero torque on the beam.
Torque applied by the car:
We can use this to find the mass of a student that will create the same amount of torque while hanging from the rope:
Example Question #1 : Torque
There is a 
Bob's mass is
Torque is defined as 
In order for the seesaw to balance, the torque applied by Bob must be equal to 
Example Question #11 : Torque
Terry is pushing a vertical lever that is attached to the floor, and he pushes 
Magnitude of torque can be found by relating the amount of force applied perpendicular to a lever arm about a point of rotation.
In this case, the force is not perpendicular, so we must take the perpendicular aspect of the force to find torque.
Plug in and solve.
Example Question #11 : Torque
From the given force and position vector, calculate the torque experienced by an object.
To calculate the torque experienced by the object, we must take the cross product of the force vector and the position vector.
Example Question #11 : Torque
You apply a force of 
None of these
The definition of torque is
Where
Theta is the angle between the direction of the force and the distance.
In this case, 
Plugging in our remaining values:
Example Question #1051 : Newtonian Mechanics
There is a steel disk of radius 
Assume
Initial angular momentum is zero
Combine equations:
Solve for
Definition of 
Combine equations:
Plug in values:
Certified Tutor
All AP Physics 1 Resources
