We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

AP Physics 1 : Circular and Rotational Motion

Study concepts, example questions & explanations for AP Physics 1

Create An Account

All AP Physics 1 Resources

7 Diagnostic Tests 170 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

← Previous 1 2 … 6 7 8 9 10 11 12 13 14 Next →

Example Question #7 : Period And Frequency

Two cars are racing side by side on a perfectly circular race track. The inner car is 450m from the center of the track. The outer car is 452m from center of the track. Both cars are traveling at $150\frac{km}{hr}$ .

How long does it take the inner car to complete a lap?

Possible Answers:

31.8s

107.8s

122s

67.8s

90.4s

Correct answer:

67.8s

Explanation:

Finding distance of lap of inner car:

$2\pi*450m=2826 m$

Convert $\frac{km}{hr}$ to $\frac{m}{s}$ :

$150\frac{km}{hr}*\frac{1000m}{1 km}*\frac{1hr}{3600s}=41.7\frac{m}{s}$

Use the distance formula:

$v=\frac{d}{t}$

$41.7=\frac{2826}{t}$

t=67.8s

Report an Error

Example Question #8 : Period And Frequency

How much longer does it take the outer car to complete one lap?

Possible Answers:

.2s

.3s

Correct answer:

.3s

Explanation:

Inner car time:

Finding distance of lap of inner car:

$2\pi*450m=2826 m$

Convert $\frac{km}{hr}$ to $\frac{m}{s}$ :

$150\frac{km}{hr}*\frac{1000m}{1 km}*\frac{1hr}{3600s}=41.7\frac{m}{s}$

Use the distance formula:

$v=\frac{d}{t}$

$41.7=\frac{2826}{t}$

t_1=67.8s

Finding distance of lap of outer car:

$2\pi*452m=2839 m$

Convert $\frac{km}{hr}$ to $\frac{m}{s}$ :

$150\frac{km}{hr}*\frac{1000m}{1 km}*\frac{1hr}{3600s}=41.7\frac{m}{s}$

Use the distance formula:

$v=\frac{d}{t}$

$41.7=\frac{2839}{t}$

t_2=68.1s

t_2-t_1=68.1-67.8=.3s

Report an Error

Example Question #9 : Period And Frequency

A car with wheels of mass 25kg and wheels of radius .25m is traveling at $50\frac{m}{s}$ . Treating the wheels as disks of uniform mass density, calculate the angular frequency of one wheel.

Possible Answers:

$100\frac{radians}{second}$

None of these

$50\frac{radians}{second}$

$400\frac{radians}{second}$

$200\frac{radians}{second}$

Correct answer:

$200\frac{radians}{second}$

Explanation:

$50\frac{m}{s}*\frac{1 rotation}{2*\pi*.25m}*\frac{2\pi radians}{rotation}=200\frac{radians}{second}$

Report an Error

Example Question #10 : Period And Frequency

A car with wheels of mass 25kg and wheels of radius .25m is traveling at $50\frac{m}{s}$ . Treating the wheels as disks of uniform mass density, calculate the angular period of one wheel.

Possible Answers:

$10\frac{seconds}{radian}$

$.005\frac{seconds}{radian}$

None of these

$5\frac{seconds}{radian}$

$.5\frac{seconds}{radian}$

Correct answer:

$.005\frac{seconds}{radian}$

Explanation:

First, find the angular frequency:

$50\frac{m}{s}*\frac{1 rotation}{2*\pi*.25m}*\frac{2\pi radians}{rotation}=200\frac{radians}{second}$

Angular period is the inverse of angular frequency:

$\frac{1}{200\frac{radians}{second}}=.005\frac{seconds}{radian}$

Report an Error

Example Question #121 : Circular And Rotational Motion

A bowling ball of mass 5kg and radius r=0.12m is thrown with a rotational kinetic energy of 20J . Find its period.

Possible Answers:

0.17s

0.77s

0.52s

0.90s

0.39s

Correct answer:

0.17s

Explanation:

The expression for rotational kinetic energy is:

$K = \frac{1}{2}Iw^2$

Where I is the moment of inertia for a solid sphere:

$I = \frac{2}{5}mr^2$

And w is the angular velocity:

$w = \frac{v}{r}$

Plugging these in, we get:

$K = \frac{1}{5}mv^2$

Rearranging for linear velocity:

$v=\sqrt{\frac{5K}{m}}$

The expression for period is the circumference of the ball divided by the linear velocity of the ball:

$P = \frac{c}{v}$

Plugging in expressions, we get:

$P = \frac{2\pi r}{\sqrt{\frac{5K}{m}}}$

$P = 2\pi r \sqrt{\frac{m}{5K}}$

We have all of these values, so time to plug and chug:

$P = 2\pi (0.12m)\sqrt{\frac{5kg}{5(20J)}}$

P = 0.17s

Report an Error

Example Question #122 : Circular And Rotational Motion

A ferris wheel has a diameter of 60 meters. The carriages on the outside of the wheel are traveling at an instantaneous velocity of $3\frac{m}{s}$ . What is the period of rotation of the wheel?

Possible Answers:

$81\ \text{seconds}$

$14\ \text{seconds}$

$63\ \text{seconds}$

$31\ \text{seconds}$

$20\ \text{seconds}$

Correct answer:

$63\ \text{seconds}$

Explanation:

We can calculate the circumference of the wheel using the given radius:

$C = 2\pi r = 2\pi \cdot30 = 60\pi\ m$

We can use this and the given velocity to find the period:

$P = \frac{C}{v} = \frac{60\pi}{3} = 63\ \text{seconds}$

Report an Error

Example Question #21 : Motion

A wheel of radius rolls along a flat floor and makes rotations over a period of time. What distance has the wheel traveled?

Possible Answers:

$n\pi r^2$

$n\pi r$

$n(2\pi r)$

$\frac{2\pi r}{n}$

$\frac{\pi r}{n}$

Correct answer:

$n(2\pi r)$

Explanation:

In order to find the distance the wheel travels, we need a way to convert angular displacement to linear displacement. We know that the circumference of a circle (or a wheel, in this case) is $2\pi r$ . This means that in one rotation, the wheel would travel a distance equal to its circumference.

Distance of one rotation equals: 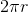$2\pi r$ .

Since the wheel travels rotations, the total distance that the wheel travels will be equal to the distance traveled by one rotation multiplied by the number of rotations.

Distance of rotations equals: $n(2\pi r)$

$d=n(2\pi r)$

Report an Error

Example Question #1 : Other Circular And Rotational Motion Concepts

A track runner who weighs 750 N is running around a curve at a speed of $4.8 \:\frac{m}{s}$ in an arc whose radius, , is 6.0 m. Find the centripetal force acting on him.

$g=10 \:\frac{m}{s^2}$

Possible Answers:

$290 \:N$

$360 \:N$

$3600 \:N$

$60 \:N$

$2900 \:N$

Correct answer:

$290 \:N$

Explanation:

The equation for centripetal force on an object moving at a constant speed in a circular path is

$F_{c}=m\frac{v^{2}}{r}$

The weight of the person is given to be $750 \:N$ . Assuming $g=10 \:\frac{m}{s^2}$ , we can find the mass of the person using the equation

$m = \frac{F_{g}}{g}=\frac{750\:N}{10\:\frac{m}{s^2}}=75 \:kg$

We are given the velocity, , and the radius, . So, we can now solve for the centripetal force:

$F_{c}=75\:kg\cdot \frac{(4.8\:\frac{m}{s})^{2}}{6.0\:m} = 290\:N$

Report an Error

Example Question #2 : Other Circular And Rotational Motion Concepts

A 55 cm rope is tied to the handle of a bucket, which is then spun in a vertical circle. The mass of the bucket is 3.3 kg. What is the minimum speed required such that the rope does not become slack when the bucket reaches the highest point in the circle?

$g=10 \:\frac{m}{s^2}$

Possible Answers:

$1.4\frac{m}{s}$

$2.3 \frac{m}{s}$

$5.5\frac{m}{s}$

$14\frac{m}{s}$

$23 \frac{m}{s}$

Correct answer:

$2.3 \frac{m}{s}$

Explanation:

The faster that the object is moving while being spun, the greater the force of tension in the rope will be. Therefore, if we want to find the minimum speed of the bucket at the highest point in the circle such that the rope doesn't go slack, we should assume that the tension at that point is zero.

If the tension is zero, then the only force acting on the bucket at that point would be the force of gravity pulling down on the bucket. If the rope does not go slack, then the bucket must still be moving in a circular motion, so we can use the equation for circular/centripetal motion:

$F_{c}=m\frac{v^{^{2}}}{r}$

Since gravity is the only force, then

$mg=m\frac{v^{2}}{r}$

We can divide by on both sides to cancel that out, and then solve for :

$g=\frac{v^{2}}{r}$

$v=\sqrt{gr}$

The radius was given to us as 55 cm. We have to convert this to meters. Since $1 \:m = 100 \:cm$ , we should divide by 100 to get $55 \:cm = 0.55 \:m$ . Now, plug that into the equation above and solve for velocity:

$v=\sqrt{10\:\frac{m}{s^2}\cdot 0.55\:m}=\sqrt{5.5\:\frac{m^2}{s^2}}=2.3\frac{m}{s}$

Report an Error

Example Question #1 : Other Circular And Rotational Motion Concepts

Bob is riding a merry-go-round. He is 10 meters from the center and the merry-go-round completes two revolutions per minute. What is the centripetal acceleration acting on Bob?

Possible Answers:

$0.44\frac{m}{s^2}$

$0.011\frac{m}{s^2}$

$40\frac{m}{s^2}$

$0.2\frac{m}{s^2}$

$5.0\frac{m}{s^2}$

Correct answer:

$0.44\frac{m}{s^2}$

Explanation:

The formula for centripetal acceleration is:

$a_c=\frac{v^2}{r}$

First, we need to solve for velocity by taking the distance Bob travels and dividing by the time it takes to travel that distance. The distance he travels is the circumference of the circle, and the time is 30 seconds, because the merry-go-round completes two revolutions per minute, or one revolution every thirty seconds:

$v=\frac{2\pi r}{T}=\frac{2\pi (10m)}{30s}=2.09 \frac{m}{s}$

Therefore,

$a_c=\frac{(2.09\frac{m}{s})^2}{10m}=0.44\frac{m}{s^2}$

Report an Error

← Previous 1 2 … 6 7 8 9 10 11 12 13 14 Next →

View AP Physics 1 Tutors

Omar
Certified Tutor

Arizona State University, Bachelors, Civil Engineering.

View AP Physics 1 Tutors

Erin
Certified Tutor

Missouri University of Science and Technology, Bachelor of Science, Physics.

View AP Physics 1 Tutors

Yousef
Certified Tutor

University of Massachusetts-Lowell, Doctor of Philosophy, Physics.

All AP Physics 1 Resources

7 Diagnostic Tests 170 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ACT Tutors in San Diego, Algebra Tutors in Philadelphia, Physics Tutors in Phoenix, Spanish Tutors in Boston, English Tutors in Houston, Chemistry Tutors in Los Angeles, Statistics Tutors in Boston, Reading Tutors in Miami, Chemistry Tutors in Chicago, LSAT Tutors in Houston

Popular Courses & Classes

GMAT Courses & Classes in New York City, ISEE Courses & Classes in San Francisco-Bay Area, SSAT Courses & Classes in San Francisco-Bay Area, GRE Courses & Classes in Los Angeles, MCAT Courses & Classes in Seattle, Spanish Courses & Classes in Denver, ISEE Courses & Classes in New York City, SAT Courses & Classes in Houston, ISEE Courses & Classes in Los Angeles, SSAT Courses & Classes in Denver

Popular Test Prep

ISEE Test Prep in Los Angeles, ISEE Test Prep in Miami, SAT Test Prep in Washington DC, GRE Test Prep in Atlanta, ISEE Test Prep in Chicago, ACT Test Prep in Houston, LSAT Test Prep in Chicago, LSAT Test Prep in Phoenix, MCAT Test Prep in Houston, LSAT Test Prep in Dallas Fort Worth

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

AP Physics 1 : Circular and Rotational Motion

Study concepts, example questions & explanations for AP Physics 1

All AP Physics 1 Resources

Example Questions

Example Question #7 : Period And Frequency

Example Question #8 : Period And Frequency

Example Question #9 : Period And Frequency

Example Question #10 : Period And Frequency

Example Question #121 : Circular And Rotational Motion

Example Question #122 : Circular And Rotational Motion

Example Question #21 : Motion

Example Question #1 : Other Circular And Rotational Motion Concepts

Example Question #2 : Other Circular And Rotational Motion Concepts

Example Question #1 : Other Circular And Rotational Motion Concepts

All AP Physics 1 Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: