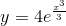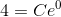Call Now to Set Up Tutoring:

(888) 888-0446

AP Calculus BC : Modeling by Solving Separable Differential Equations

Study concepts, example questions & explanations for AP Calculus BC

Create An Account

All AP Calculus BC Resources

2 Diagnostic Tests 86 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #191 : Ap Calculus Bc

Solve the separable differential equation

$\frac{\mathrm{d} y}{\mathrm{d} x}= yx^2$ $\displaystyle \frac{\mathrm{d} y}{\mathrm{d} x}= yx^2$

with the condition y(0)=4 $\displaystyle y(0)=4$.

Possible Answers:

$y=Ce^{\frac{x^2}{2}}$ $\displaystyle y=Ce^{\frac{x^2}{2}}$

$y=4e^{\frac{x^2}{3}}$ $\displaystyle y=4e^{\frac{x^2}{3}}$

$y=4e^{\frac{x^3}{3}}$ $\displaystyle y=4e^{\frac{x^3}{3}}$

$y=Ce^{\frac{64}{3}}$ $\displaystyle y=Ce^{\frac{64}{3}}$

$y=Ce^{\frac{x^3}{3}}$ $\displaystyle y=Ce^{\frac{x^3}{3}}$

Correct answer:

$y=4e^{\frac{x^3}{3}}$ $\displaystyle y=4e^{\frac{x^3}{3}}$

Explanation:

To solve the separable differential equation, we must separate x and y, dx and dy respectively to opposite sides:

$\frac{dy}{y}=x^2dx$ $\displaystyle \frac{dy}{y}=x^2dx$

Integrating both sides, we get

$\ln\left | y\right |=\frac{ x^3}{3}+C$ $\displaystyle \ln\left | y\right |=\frac{ x^3}{3}+C$

The rules of integration used were

$\int \frac{dx}{x}=\ln\left | x\right |+C$ $\displaystyle \int \frac{dx}{x}=\ln\left | x\right |+C$, $\int x^ndx= \frac{x^{n+1}}{n+1}+C$ $\displaystyle \int x^ndx= \frac{x^{n+1}}{n+1}+C$

The constants of integration merged into one.

Now, we exponentiate both sides of the equation to solve for y, and use the properties of exponents to simplify:

$y=e^{\frac{x^3}{3}}+e^C=e^{{\frac{x^3}{3}}\cdot C}=Ce^{\frac{x^3}{3}}$ $\displaystyle y=e^{\frac{x^3}{3}}+e^C=e^{{\frac{x^3}{3}}\cdot C}=Ce^{\frac{x^3}{3}}$

To solve for C, we use our given condition:

4=Ce^0 $\displaystyle 4=Ce^0$

4=C $\displaystyle 4=C$

Our final answer is

$y=4e^{\frac{x^3}{3}}$ $\displaystyle y=4e^{\frac{x^3}{3}}$

Report an Error

View AP Calculus BC Tutors

Bertha
Certified Tutor

California Institute of Technology, Bachelor's (in progress), Chemical Engineering.

View AP Calculus BC Tutors

Harrison
Certified Tutor

Hamilton College, Bachelor in Arts, Mathematics. University of Connecticut, Master of Science, Applied Mathematics.

View AP Calculus BC Tutors

Wyatt
Certified Tutor

Embry-Riddle Aeronautical University-Prescott, Bachelor of Engineering, Mechanical Engineering.

All AP Calculus BC Resources

2 Diagnostic Tests 86 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SSAT Tutors in Miami, ISEE Tutors in Chicago, Calculus Tutors in Seattle, French Tutors in Los Angeles, Chemistry Tutors in Atlanta, ISEE Tutors in Seattle, English Tutors in New York City, Spanish Tutors in Dallas Fort Worth, Calculus Tutors in Boston, Math Tutors in Seattle

Popular Courses & Classes

ACT Courses & Classes in Boston, GMAT Courses & Classes in San Francisco-Bay Area, Spanish Courses & Classes in Atlanta, LSAT Courses & Classes in Phoenix, ISEE Courses & Classes in Los Angeles, ISEE Courses & Classes in San Diego, Spanish Courses & Classes in Houston, SAT Courses & Classes in Los Angeles, GRE Courses & Classes in Denver, SSAT Courses & Classes in Miami

Popular Test Prep

GRE Test Prep in Atlanta, GMAT Test Prep in Atlanta, ISEE Test Prep in Los Angeles, GMAT Test Prep in Phoenix, GRE Test Prep in Miami, LSAT Test Prep in Phoenix, SSAT Test Prep in Boston, ISEE Test Prep in Boston, SAT Test Prep in Seattle, MCAT Test Prep in Denver

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

AP Calculus BC : Modeling by Solving Separable Differential Equations

Study concepts, example questions & explanations for AP Calculus BC

All AP Calculus BC Resources

Example Questions

Example Question #191 : Ap Calculus Bc

All AP Calculus BC Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: