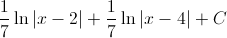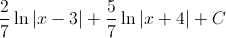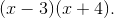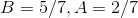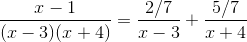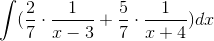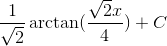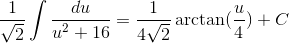Call Now to Set Up Tutoring:

(888) 888-0446

AP Calculus BC : Fundamental Theorem of Calculus and Techniques of Antidifferentiation

Study concepts, example questions & explanations for AP Calculus BC

Create An Account

All AP Calculus BC Resources

2 Diagnostic Tests 86 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

← Previous 1 2 Next →

Example Question #11 : Fundamental Theorem Of Calculus And Techniques Of Antidifferentiation

Evaluate the following integral

$\int_0^5 3x^4-12x^3+10x+12dx$

Possible Answers:

185

685

1875

625

Correct answer:

185

Explanation:

Evaluate the following integral

$\int_0^5 3x^4-12x^3+10x+12dx$

Let's begin by recalling our "reverse power rule" AKA, the antiderivative form of our power rule.

$\int x^ndx=\frac{x^{n+1}}{n+1}+c$

In other words, all we need to do for each term is increase the exponent by 1 and then divide by that number.

$\int_0^5 3x^4-12x^3+10x+12dx=\frac{3x^5}{5}-\frac{12x^4}{4}+\frac{10x^2}{2}+12x+c\mid_0^5$

Let's clean it up a little to get:

$\frac{3x^5}{5}-3x^4+5x^2+12x+c\mid_0^5$

Now, to evaluate our integral, we need to plug in 5 and 0 for x and find the difference between the values. In other words, if our integrated function is F(x), we need to find F(5)-F(0).

Let's start with F(5)

$\frac{3(5)^5}{5}-3(5)^4+5(5)^2+12(5)+c=1875-1875+125+60+c=185+c$

Next, let's look at F(0). If you look at our function carefully, you will notice that F(0) will cancel out all of our terms except for +c. So, we have the following:

F(5)=185+c

F(0)=c

Finding the difference cancels out the c's and leaves us with 185.

185+c-c=185

Report an Error

Example Question #531 : Finding Integrals

Evaluate:

$\int_{0}^{\infty } \frac{\cos x\; \mathrm{d}x}{e^{x}}$

Possible Answers:

$\frac{1}{e}$

$\frac{\sqrt{2}}{2e}$

$\frac{1}{2}$

$\frac{1}{2e}$

Correct answer:

$\frac{1}{2}$

Explanation:

First, we will find the indefinite integral $\int \frac{\cos x\; \mathrm{d}x}{e^{x}} = \int e^{-x} \cos x\; \mathrm{d}x$ using integration by parts.

We will let $u = \cos x$ and $\mathrm{d}v= e^{-x}\; \mathrm{d}x$ .

Then $\frac{\mathrm{d} u}{\mathrm{d} x} = - \sin x$ and $\mathrm{d} u = - \sin x \; \mathrm{d} x$ .

$v= \int e^{-x}\; \mathrm{d}x = - e^{-x} = - \frac{1}{e^{x} }$

$\int \frac{\cos x\; \mathrm{d}x}{e^{x}} = \int e^{-x} \cos x\; \mathrm{d}x$

$=\int u \; \mathrm{d} v$

$= uv - \int v \; \mathrm{d} u$

$= \cos x \cdot \left (- \frac{1}{e^{x} } \right ) - \int \left (- \frac{1}{e^{x} } \right ) \; \cdot \left (- \sin x \right )\; \mathrm{d} x$

$= - \frac{\cos x}{e^{x} } - \int e^{-x} \sin x \; \mathrm{d} x$

To find $\int e^{-x} \sin x \; \mathrm{d} x$ , we use another integration by parts:

$u = \sin x$ , which means that $\mathrm{d} u = \cos x \; \mathrm{d} x$ , and

$\mathrm{d}v= e^{-x}\; \mathrm{d}x$ , which means that, again, $v= - \frac{1}{e^{x} }$ .

$\int e^{-x} \sin x \; \mathrm{d} x$

$=\int u \; \mathrm{d} v$

$= uv - \int v \; \mathrm{d} u$

$= \sin x \cdot \left (- \frac{1}{e^{x} } \right ) - \int \left (- \frac{1}{e^{x} } \right ) \; \cdot \cos x \; \mathrm{d} x$

$= - \frac{ \sin x }{e^{x} } + \int \frac{\cos x \; \mathrm{d} x}{e^{x} }$

$\int \frac{\cos x\; \mathrm{d}x}{e^{x}} = - \frac{\cos x}{e^{x} } - \int e^{-x} \sin x \; \mathrm{d} x$

$\int \frac{\cos x\; \mathrm{d}x}{e^{x}} = - \frac{\cos x}{e^{x} } - \left ( - \frac{ \sin x }{e^{x} } + \int \frac{\cos x \; \mathrm{d} x}{e^{x} } \right )$

$\int \frac{\cos x\; \mathrm{d}x}{e^{x}} = - \frac{\cos x}{e^{x} } + \frac{ \sin x }{e^{x} } - \int \frac{\cos x \; \mathrm{d} x}{e^{x} }$

$2 \int \frac{\cos x\; \mathrm{d}x}{e^{x}} = - \frac{\cos x}{e^{x} } + \frac{ \sin x }{e^{x} }$

$2 \int \frac{\cos x\; \mathrm{d}x}{e^{x}} = \frac{\sin x -\cos x}{e^{x} }$

$\int \frac{\cos x\; \mathrm{d}x}{e^{x}} = \frac{\sin x -\cos x}{2e^{x} }$

Since

$\frac{-2}{2e^{x} } \leq \frac{\sin x -\cos x}{2e^{x} } \leq \frac{2}{2e^{x} }$ , or,

$- \frac{1}{e^{x} } \leq \frac{\sin x -\cos x}{2e^{x} } \leq \frac{1}{e^{x} }$

for all real , and

$- \lim_{x\rightarrow \infty } \frac{1}{e^{x} } = \lim_{x\rightarrow \infty } \frac{1}{e^{x} } = 0$ ,

by the Squeeze Theorem,

$\lim_{x\rightarrow \infty } \frac{\sin x -\cos x}{2e^{x} } = 0$ .

$\int_{0}^{\infty } \frac{\cos x\; \mathrm{d}x}{e^{x}}$

$= \lim_{b\rightarrow \infty }\int_{0}^{b } \frac{\cos x\; \mathrm{d}x}{e^{x}}$

$= \lim_{ b\rightarrow \infty }$ $\left.\begin{matrix} \frac{\sin x -\cos x}{2e^{x} } \\ \textrm{ } \end{matrix}\right|$ $\begin{matrix} b\\ \\ 0 \end{matrix}$

$= 0 - \frac{\sin 0 -\cos 0}{2e^{0} }$

$= - \frac{ 0 -1}{2 \cdot 1 } = \frac{1}{2}$

Report an Error

Example Question #2631 : Calculus Ii

Evaluate:

$\int_{0}^{1} x \ln x \; \mathrm{d}x$

Possible Answers:

$-\ln 4$

$-\frac{1}{4}$

$\ln 4$

$\frac{1}{4}$

The integral does not converge

Correct answer:

$-\frac{1}{4}$

Explanation:

First, we will find the indefinite integral, $\int x \ln x \; \mathrm{d}x$ .

We will let $u = \ln x$ and $\mathrm{d}v= x \; \mathrm{d}x$ .

Then,

$\frac{\mathrm{d} u }{\mathrm{d} x}= \frac{1}{x}$ and $\mathrm{d} u = \frac{\mathrm{d} x}{x}$ .

$v= \int x \; \mathrm{d}x =\frac{ x ^{2}}{2}$

and

$\int x \ln x \; \mathrm{d}x$

$=\int u \; \mathrm{d} v$

$= uv - \int v \; \mathrm{d} u$

$= \ln{x} \cdot \frac{ x ^{2}}{2} - \int \left (\frac{ x ^{2}}{2} \right ) \frac{\mathrm{d} x}{x}$

$= \frac{ x ^{2}\ln{x}}{2} - \frac{1}{2}\int x\; \mathrm{d} x$

$= \frac{ x ^{2}\ln{x}}{2} - \frac{1}{2} \cdot \frac{x^{2}}{2}$

$= \frac{ x ^{2}\ln{x}}{2} - \frac{x^{2}}{4}$

Now, this expression evaluated at x = 1 is equal to

$\frac{ 1 ^{2}\ln{1}}{2} - \frac{1^{2}}{4} = 0 - \frac{1}{4} = - \frac{1}{4}$ .

At x = 0 it is undefined, because $\ln 0$ does not exist.

We can use L'Hospital's rule to find its limit as $x\rightarrow 0$ , as follows:

$\lim_{x\rightarrow 0}\frac{2 x ^{2}\ln{x} - x^{2}}{4} =\lim_{x\rightarrow 0} \frac{2 \ln{x} - 1}{\frac{4}{x ^{2}}}$

$\lim_{x\rightarrow 0} \left (2 \ln{x} - 1 \right ) = - \infty$ and $\lim_{x\rightarrow 0} \frac{4}{x ^{2}} = \infty$ , so by L'Hospital's rule,

$\lim_{x\rightarrow 0} \frac{2 \ln{x} - 1}{\frac{4}{x ^{2}}}=\lim_{x\rightarrow 0} \frac{\frac {2}{x} }{\frac{-8}{x ^{3}}} = \lim_{x\rightarrow 0}\left ( -\frac{x^{2}}{4} \right ) = 0$

Therefore,

$\int_{0}^{1} x \ln x \; \mathrm{d}x$

$= \left.\begin{matrix} \frac{ x ^{2}\ln{x}}{2} - \frac{x^{2}}{4} \\ \\ \end{matrix}\right| \begin{matrix} 1\\ \\ 0 \end{matrix}$

$=\lim _{b\rightarrow 0}\left [ \left.\begin{matrix} \frac{ x ^{2}\ln{x}}{2} - \frac{x^{2}}{4} \\ \\ \end{matrix}\right| \begin{matrix} 1\\ \\ b \end{matrix} \right ]$

$= -\frac{1}{4} - 0$

$= -\frac{1}{4}$

Report an Error

Example Question #1 : Improper Integrals

Evaluate:

$\int_{0 }^{\infty} \frac{x\; \mathrm{d}x}{e^{x^{2}}}$

Possible Answers:

$\frac{e}{2}$

$\frac{1}{2}$

$\frac{2}{e}$

Correct answer:

$\frac{1}{2}$

Explanation:

Rewrite the integral as

$\int_{0 }^{\infty} \frac{x\; \mathrm{d}x}{e^{x^{2}}} = \int_{0 }^{\infty}e^{-x^{2}}\cdot x \; \mathrm{d}x} }$ .

Substitute $u = - x^{2}$ . Then

$\frac{\mathrm{d} u}{\mathrm{d} x} = - 2x$ and $-\frac{1}{2} \mathrm{d} u = x \; \mathrm{d} x$ . The lower bound of integration stays $u = - 0^{2} = 0$ , and the upper bound becomes $\lim_{x\rightarrow \infty } - x^{2} = - \infty$ , so

$\int_{0 }^{\infty} \frac{x\; \mathrm{d}x}{e^{x^{2}}} = \int_{0 }^{\infty}e^{-x^{2}}\cdot x \; \mathrm{d}x} }=-\frac{1}{2} \int_{0 }^{-\infty}e^{u} \mathrm{d}u}= \frac{1}{2} \int_{-\infty }^{0}e^{u} \mathrm{d}u}$

$=\frac{1}{2} \lim_{b\rightarrow -\infty } \left.\begin{matrix} e ^{u}\\ \textrm{ } \\ \textrm{ } \end{matrix}\right| \begin{matrix} 0\\ \\ b \end{matrix}$

Since $\lim_{b\rightarrow -\infty } e ^{u} = 0$ , the above is equal to

$=\frac{1}{2} (e^{0}-0) =\frac{1}{2} (1) = \frac{1}{2}$ .

Report an Error

Example Question #4 : Improper Integrals

Evaluate $\int_{1}^{\infty}\frac{4}{x^{5}}dx$ .

Possible Answers:

$\infty$

$-\infty$

Correct answer:

Explanation:

By the Formula Rule, we know that $\int_{a}^{\infty}F(x)dx=\lim_{b\rightarrow \infty}\int_{a}^{b}f(x)dx$ . We therefore know that $\int_{1}^{\infty}\frac{4}{x^{5}}dx=\lim_{b\rightarrow \infty}\int_{1}^{b}\frac{4}{x^{5}}dx$ .

Continuing the calculation:

$\int_{1}^{b}\frac{4}{x^{5}}dx$

$=4\int_{1}^{b}\frac{1}{x^{5}}dx$

$=4\int_{1}^{b}{x^{-5}}dx$

By the Power Rule for Integrals, $\int x^{n}dx=\frac{x^{n+1}}{n+1}+C$ for all $n\neq-1$ with an arbitrary constant of integration . Therefore:

$4\int_{1}^{b}{x^{-5}}dx$

$=4({\frac{x^{-5+1}}{-5+1}})_{1}^{b}$

$=4(\frac{x^{-4}}{-4}})_{1}^{b}$

$=4(-{\frac{1}{4x^{4}}})_{1}^b$ .

So, $\lim_{b\rightarrow \infty }4(-{\frac{1}{4x^{4}}})_{1}^b$

$=\lim_{b\rightarrow \infty }4[-{\frac{1}{4b^{4}}-(-\frac{1}{4}})]$

$=\lim_{b\rightarrow \infty }4[-{\frac{1}{4b^{4}}+\frac{1}{4}})]$

$=\lim_{b\rightarrow \infty }[-{\frac{1}{b^{4}}+1}]$ .

=0+1

Report an Error

Example Question #1 : Substitution Of Variables (By Parts And Simple Partial Fractions)

$\int\frac{x-1}{(x-3)(x+4)} dx=$

Possible Answers:

$\frac{5}{7(x+4)}\ln |x|+\frac{2}{7(x-3)}\ln |x|+C$

$\frac{2}{7}\ln|x-3|+\frac{5}{7}\ln| x+4|+C$

$\frac{(x-3)^2}{}7+\frac{2(x+4)^2}{7}+C$

$\frac{5}{7(x+4)}+\frac{2}{7(x+2)}+C$

$\frac{1}{7}\ln|x-2|+\frac{1}{7}\ln|x-4|+C$

Correct answer:

$\frac{2}{7}\ln|x-3|+\frac{5}{7}\ln| x+4|+C$

Explanation:

In order to evaluate this integral, we will need to use partial fraction decomposition.

$\frac{x-1}{(x-3)(x+4)}=\frac{A}{x-3}+\frac{B}{x+4}$

Multiply both sides of the equation by the common denominator, which is (x-3)(x+4).

x-1=A(x+4)+B(x-3)

x-1=Ax+4A+Bx-3B=(A+B)x+4A-3B

This means that A+B must equal 1, and 4A-3B=-1.

A+B=1

A=1-B

4(1-B)-3B=-1

B=5/7, A=2/7

$\frac{x-1}{(x-3)(x+4)}=\frac{2/7}{x-3}+\frac{5/7}{x+4}$

$\int(\frac{2}{7}\cdot \frac{1}{x-3}+\frac{5}{7}\cdot \frac{1}{x+4})dx$

$=\int\frac{2}{7}\cdot\frac{1}{x-3} dx +\int\frac{5}{7}\cdot\frac{1}{x+4}dx$

$=\frac{2}{7}\int\frac{dx}{x-3}+\frac{5}{7}\int\frac{dx}{x+4}$

$=\frac{2}{7}\ln|x-3|+\frac{5}{7}\ln| x+4|+C$

The answer is $\frac{2}{7}\ln|x-3|+\frac{5}{7}\ln| x+4|+C$ .

Report an Error

Example Question #1 : Substitution Of Variables (By Parts And Simple Partial Fractions)

Integrate:

$\int \frac{dx}{2x^2+16}$

Possible Answers:

$\frac{1}{4\sqrt{2}}\arctan(\frac{x}{4})+C$

$\frac{1}{4\sqrt{2}}\arcsin(\frac{x}{4})+C$

$\frac{1}{\sqrt{2}}\arctan(\frac{\sqrt{2}x}{4})+C$

$\arccos(\frac{x}{4})+C$

$\frac{1}{4\sqrt{2}}\arctan(\frac{\sqrt{2}x}{4})+C$

Correct answer:

$\frac{1}{4\sqrt{2}}\arctan(\frac{\sqrt{2}x}{4})+C$

Explanation:

To integrate, we must first make the following substitution:

$u=\sqrt{2}x, du=\sqrt{2}dx$

Rewriting the integral in terms of u and integrating, we get

$\frac{1}{\sqrt{2}}\int \frac{du}{u^2+16}= \frac{1}{4\sqrt{2}}\arctan(\frac{u}{4})+C$

The following rule was used to integrate:

$\int \frac{du}{u^2+a^2}=\frac{1}{a}\arctan(\frac{x}{a})+C$

Finally, we replace u with our original x term:

$\frac{1}{4\sqrt{2}}\arctan(\frac{\sqrt{2}x}{4})+C$

Report an Error

← Previous 1 2 Next →

View AP Calculus BC Tutors

Pankaj
Certified Tutor

University of Delhi, Electrical Engineer, Electrical Engineering. Columbia University in the City of New York, Master of Arts...

View AP Calculus BC Tutors

Brianna
Certified Tutor

Cedarville University, Bachelor of Science, Civil Engineering.

View AP Calculus BC Tutors

Yuliya
Certified Tutor

University of Maryland-College Park, Bachelor of Science, Mathematics. George Washington University, Masters in Education, Ed...

All AP Calculus BC Resources

2 Diagnostic Tests 86 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Calculus Tutors in San Diego, SAT Tutors in Denver, Chemistry Tutors in Atlanta, GRE Tutors in Washington DC, MCAT Tutors in Miami, SAT Tutors in Dallas Fort Worth, Biology Tutors in Philadelphia, Biology Tutors in Denver, Math Tutors in Atlanta, MCAT Tutors in Atlanta

Popular Courses & Classes

ISEE Courses & Classes in Atlanta, ACT Courses & Classes in Miami, GMAT Courses & Classes in San Diego, MCAT Courses & Classes in Washington DC, ISEE Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in Boston, Spanish Courses & Classes in Seattle, SAT Courses & Classes in Washington DC, LSAT Courses & Classes in Los Angeles, GRE Courses & Classes in Boston

Popular Test Prep

ISEE Test Prep in Los Angeles, ISEE Test Prep in San Francisco-Bay Area, SSAT Test Prep in San Francisco-Bay Area, GRE Test Prep in Phoenix, GMAT Test Prep in Washington DC, ISEE Test Prep in Houston, LSAT Test Prep in Houston, SSAT Test Prep in Boston, ACT Test Prep in San Francisco-Bay Area, GMAT Test Prep in Dallas Fort Worth

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

AP Calculus BC : Fundamental Theorem of Calculus and Techniques of Antidifferentiation

Study concepts, example questions & explanations for AP Calculus BC

All AP Calculus BC Resources

Example Questions

Example Question #11 : Fundamental Theorem Of Calculus And Techniques Of Antidifferentiation

Example Question #531 : Finding Integrals

Example Question #2631 : Calculus Ii

Example Question #1 : Improper Integrals

Example Question #4 : Improper Integrals

Example Question #1 : Substitution Of Variables (By Parts And Simple Partial Fractions)

Example Question #1 : Substitution Of Variables (By Parts And Simple Partial Fractions)

All AP Calculus BC Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: