All AP Calculus AB Resources
Example Questions
Example Question #201 : Integrals
Example Question #202 : Integrals
Example Question #21 : Riemann Sums (Left, Right, And Midpoint Evaluation Points)
Example Question #22 : Riemann Sums (Left, Right, And Midpoint Evaluation Points)
Example Question #23 : Riemann Sums (Left, Right, And Midpoint Evaluation Points)
Example Question #24 : Riemann Sums (Left, Right, And Midpoint Evaluation Points)
Example Question #201 : Integrals
Let 
A relative maximum of the graph of 
The graph of 
At a relative minimum 



First, find 
Differentiate the individual terms using the Constant Multiple and Power Rules:
Set this equal to 0:
Either:





Now take the second derivative, again using the sum rule:
Differentiate the individual terms using the Constant Multiple and Power Rules:
Substitute 

Therefore, 

Now. substitute 

Therefore, 

Example Question #26 : Riemann Sums (Left, Right, And Midpoint Evaluation Points)
Estimate the integral of 
Because our 
Example Question #27 : Riemann Sums (Left, Right, And Midpoint Evaluation Points)
Use Left Riemann sums with 4 subintervals to approximate the area between the x-axis, 


To use left Riemann sums, we need to use the following formula:

where 



,
and 

This fancy equation approximates using boxes. We can rewrite this fancy equation by writing 




Think of 

This is basically 
Now we need to determine what 

To find 


In short,
Now we need to find the x values that are the left endpoints of each of the 4 subintervals. Left endpoints because we are doing Left Riemann sums.
The left most x value happens to be the smaller of the overall endpoints given in the question. In other words, since we only care about the area from 



Now we know that 
To find the next endpoint, 

Add the 
And repeat to find
Now that we have all the pieces, we can plug them in.
plug each value into 
This is the final answer, which is an approximation of the area under the function.
Example Question #1 : Antiderivatives By Substitution Of Variables
Use a change of variable (aka a u-substitution) to evaluate the integral,
Integrals such as this are seen very commonly in introductory calculus courses. It is often useful to look for patterns such as the fact that the polynomial under the radical in our example, 


Now differentiate with respect to 


Looking at equation (2), we can solve for 


Now proceed with the integration with respect to 

Now write the result in terms of 
Certified Tutor
Certified Tutor
All AP Calculus AB Resources






![\begin{align*}&\text{A Riemann sum integral approximation over an interval [a, b]}\\&\text{with n subintervals follows the form:}\\&\int_a^b f(x)dx \approx \frac{b-a}{n}(f(x_1)+f(x_2)+...+f(x_n))\\&\text{It is essentially a sum of n rectangles, each with a base of}\\&\text{length :}\frac{b-a}{n}\text{ and variable heights :}f(x_i)\text{, which depend on the function value at }x_i\\&\text{In our case, we have function values over an interval:}\\&f(0)=10\\&f(4)=3\\&f(8)=10\\&f(12)=-11\\&f(16)=10\\&\text{Although the total interval has a length of }16\\&\text{Notice the points are equidistant, with }4\text{ intervals between.}\\&\text{Each equidistant interval has length: }4\\&\text{Since we are using the left point of each interval, we disregard the larst function value:}\\&\int_{0}^{16}f(x)\approx4[(10)+(3)+(10)+(-11)]\\&\int_{0}^{16}f(x)\approx48\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/945108/gif.latex)
![\begin{align*}&\text{The function }f(x)\text{ has the following values on the interval }x=[-5,5]:\\&f(-5)=-5\\&f(-3)=8\\&f(-1)=4\\&f(1)=12\\&f(3)=-5\\&f(5)=-12\\&\text{Approximate the integral of }f(x)\text{ on this interval using left Riemann sums.}\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/945105/gif.latex)




![\begin{align*}&\text{A Riemann sum integral approximation over an interval [a, b]}\\&\text{with n subintervals follows the form:}\\&\int_a^b f(x)dx \approx \frac{b-a}{n}(f(x_1)+f(x_2)+...+f(x_n))\\&\text{It is essentially a sum of n rectangles, each with a base of}\\&\text{length :}\frac{b-a}{n}\text{ and variable heights :}f(x_i)\text{, which depend on the function value at }x_i\\&\text{In our case, we have function values over an interval:}\\&f(-5)=-5\\&f(-3)=8\\&f(-1)=4\\&f(1)=12\\&f(3)=-5\\&f(5)=-12\\&\text{Although the total interval has a length of }10\\&\text{Notice the points are equidistant, with }5\text{ intervals between.}\\&\text{Each equidistant interval has length: }2\\&\text{Since we are using the left point of each interval, we disregard the larst function value:}\\&\int_{-5}^{5}f(x)\approx2[(-5)+(8)+(4)+(12)+(-5)]\\&\int_{-5}^{5}f(x)\approx28\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/945106/gif.latex)
![\begin{align*}&\text{The function }f(x)\text{ has the following values on the interval }x=[-4,11]:\\&f(-4)=2\\&f(-1)=-11\\&f(2)=6\\&f(5)=-1\\&f(8)=-14\\&f(11)=12\\&\text{Approximate the integral of }f(x)\text{ on this interval using left Riemann sums.}\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/945111/gif.latex)




![\begin{align*}&\text{A Riemann sum integral approximation over an interval [a, b]}\\&\text{with n subintervals follows the form:}\\&\int_a^b f(x)dx \approx \frac{b-a}{n}(f(x_1)+f(x_2)+...+f(x_n))\\&\text{It is essentially a sum of n rectangles, each with a base of}\\&\text{length :}\frac{b-a}{n}\text{ and variable heights :}f(x_i)\text{, which depend on the function value at }x_i\\&\text{In our case, we have function values over an interval:}\\&f(-4)=2\\&f(-1)=-11\\&f(2)=6\\&f(5)=-1\\&f(8)=-14\\&f(11)=12\\&\text{Although the total interval has a length of }15\\&\text{Notice the points are equidistant, with }5\text{ intervals between.}\\&\text{Each equidistant interval has length: }3\\&\text{Since we are using the left point of each interval, we disregard the larst function value:}\\&\int_{-4}^{11}f(x)\approx3[(2)+(-11)+(6)+(-1)+(-14)]\\&\int_{-4}^{11}f(x)\approx-54\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/945112/gif.latex)



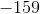

![\begin{align*}&\text{A Riemann sum integral approximation over an interval [a, b]}\\&\text{with n subintervals follows the form:}\\&\int_a^b f(x)dx \approx \frac{b-a}{n}(f(x_1)+f(x_2)+...+f(x_n))\\&\text{It is essentially a sum of n rectangles, each with a base of}\\&\text{length :}\frac{b-a}{n}\text{ and variable heights :}f(x_i)\text{, which depend on the function value at }x_i\\&\text{In our case, we have function values over an interval:}\\&f(-2)=-17\\&f(1)=-4\\&f(4)=-16\\&f(7)=-16\\&\text{Although the total interval has a length of }9\\&\text{Notice the points are equidistant, with }3\text{ intervals between.}\\&\text{Each equidistant interval has length: }3\\&\text{Since we are using the left point of each interval, we disregard the larst function value:}\\&\int_{-2}^{7}f(x)\approx3[(-17)+(-4)+(-16)]\\&\int_{-2}^{7}f(x)\approx-111\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/945098/gif.latex)





![\begin{align*}&\text{A Riemann sum integral approximation over an interval [a, b]}\\&\text{with n subintervals follows the form:}\\&\int_a^b f(x)dx \approx \frac{b-a}{n}(f(x_1)+f(x_2)+...+f(x_n))\\&\text{It is essentially a sum of n rectangles, each with a base of}\\&\text{length :}\frac{b-a}{n}\text{ and variable heights :}f(x_i)\text{, which depend on the function value at }x_i\\&\text{In our case, we have function values over an interval:}\\&f(5)=-3\\&f(11)=8\\&f(17)=11\\&f(23)=-3\\&\text{Although the total interval has a length of }18\\&\text{Notice the points are equidistant, with }3\text{ intervals between.}\\&\text{Each equidistant interval has length: }6\\&\text{Since we are using the left point of each interval, we disregard the larst function value:}\\&\int_{5}^{23}f(x)\approx6[(-3)+(8)+(11)]\\&\int_{5}^{23}f(x)\approx96\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/945125/gif.latex)





![\begin{align*}&\text{A Riemann sum integral approximation over an interval [a, b]}\\&\text{with n subintervals follows the form:}\\&\int_a^b f(x)dx \approx \frac{b-a}{n}(f(x_1)+f(x_2)+...+f(x_n))\\&\text{It is essentially a sum of n rectangles, each with a base of}\\&\text{length :}\frac{b-a}{n}\text{ and variable heights :}f(x_i)\text{, which depend on the function value at }x_i\\&\text{In our case, we have function values over an interval:}\\&f(-8)=-10\\&f(1)=12\\&f(10)=-1\\&f(19)=11\\&\text{Although the total interval has a length of }27\\&\text{Notice the points are equidistant, with }3\text{ intervals between.}\\&\text{Each equidistant interval has length: }9\\&\text{Since we are using the left point of each interval, we disregard the larst function value:}\\&\int_{-8}^{19}f(x)\approx9[(-10)+(12)+(-1)]\\&\int_{-8}^{19}f(x)\approx9\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/945129/gif.latex)

![x= \sqrt[4]{5}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/971492/gif.latex)
![x=- \sqrt[4]{5}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/971493/gif.latex)















































+[(-1)^4+1](1)+ [(0)^4+1](1)+[(1)^4+1](1)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1061094/gif.latex)
![[16 + 1]+ [1 + 1]+ [0+ 1]+ [1 + 1]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1061095/gif.latex)






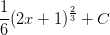
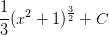


![= \frac{1}{2}\left[\frac{1}{\frac{1}{2}+1}u^{\frac{1}{2}+1} \right ]+C](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/741662/gif.latex)







